Page 303 - Biomedical Engineering and Design Handbook Volume 2, Applications

THE PRINCIPLES OF X-RAY COMPUTED TOMOGRAPHY 281

be sampled at least twice during each cycle of the highest signal frequency. This means that if a
signal x(t) has a Fourier transform such that
w
Xw() = 0 for w N (10.51)
2
samples of x must be taken at a rate greater than w , so that we require 2p/t ≥ w .
N N
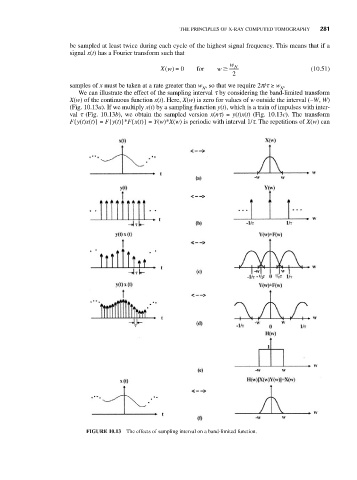
We can illustrate the effect of the sampling interval t by considering the band-limited transform
X(w) of the continuous function x(t). Here, X(w) is zero for values of w outside the interval (−W, W)
(Fig. 10.13a). If we multiply x(t) by a sampling function y(t), which is a train of impulses with inter-
val t (Fig. 10.13b), we obtain the sampled version x(nt) = y(t)x(t) (Fig. 10.13c). The transform
F{y(t)x(t)} = F{y(t)}*F{x(t)} = Y(w)*X(w) is periodic with interval 1/t. The repetitions of X(w) can

FIGURE 10.13 The effects of sampling interval on a band-limited function.