Page 71 - Circuit Analysis II with MATLAB Applications

Quality Factor Q in Series Resonance
0s

Then, by definition

Z L 1
0
Q 0S = --------- = -------------- (2.9)
R
Z RC
0
Quality Factor at Series Resonance
In a practical circuit, the resistance in the definition of Q 0S above, represents the resistance of the
R
inductor and thus the quality factor Q 0S is a measure of the energy storage property of the inductance
L in relation to the energy dissipation property of the resistance of that inductance.R

In terms of Q 0S , the magnitude of the voltages across the inductor and capacitor are

V L0 = V C0 = Q 0S V S (2.10)

and therefore, we say that there is a “resonant” rise in the voltage across the reactive devices and it is
equal to the Q 0S times the applied voltage. Thus in Example 2.1,

V V 1000 25
L0
C0
Q 0S = ------------ = ------------ = ------------ = ------
120
3
V
V
S
S
The quality factor is also a measure of frequency selectivity. Thus, we say that a circuit with a high
Q
Q
Q has a high selectivity, whereas a low circuit has low selectivity. The high frequency selectivity is
more desirable in parallel circuits as we will see in the next section.
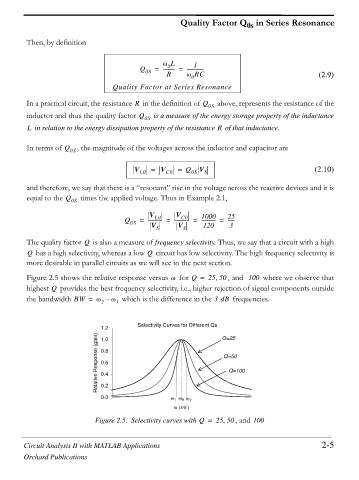
Figure 2.5 shows the relative response versus for Q = 25 50 , and 100 where we observe that

Z
highest provides the best frequency selectivity, i.e., higher rejection of signal components outside
Q
the bandwidth BW = Z – Z 1 which is the difference in the 3dB frequencies.
2
Selectivity Curves for Different Qs
1.2 Q=25
Relative Response (gain) 0.8 Q=50
1.0
0.6
Q=100
0.4
0.2
0.0 Z 1 Z 0 Z 2
Z r/s
Figure 2.5. Selectivity curves with Q = 25 50 , and 100

Circuit Analysis II with MATLAB Applications 2-5
Orchard Publications