Page 136 - Computational Modeling in Biomedical Engineering and Medical Physics

Electrical activity of the heart 125

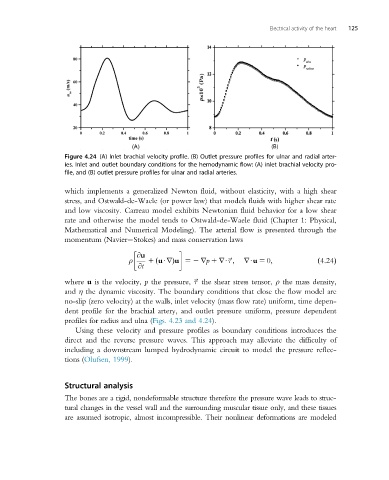
Figure 4.24 (A) Inlet brachial velocity profile. (B) Outlet pressure profiles for ulnar and radial arter-
ies. Inlet and outlet boundary conditions for the hemodynamic flow: (A) inlet brachial velocity pro-
file, and (B) outlet pressure profiles for ulnar and radial arteries.

which implements a generalized Newton fluid, without elasticity, with a high shear
stress, and Ostwald-de-Waele (or power law) that models fluids with higher shear rate
and low viscosity. Carreau model exhibits Newtonian fluid behavior for a low shear
rate and otherwise the model tends to Ostwald-de-Waele fluid (Chapter 1: Physical,
Mathematical and Numerical Modeling). The arterial flow is presented through the
momentum (Navier Stokes) and mass conservation laws

@u
ρ 1 uUrÞu 52 rp 1 rU~; rUu 5 0;
τ
@t ð ð4:24Þ
τ
where u is the velocity, p the pressure, ~ the shear stress tensor, ρ the mass density,
and η the dynamic viscosity. The boundary conditions that close the flow model are
no-slip (zero velocity) at the walls, inlet velocity (mass flow rate) uniform, time depen-
dent profile for the brachial artery, and outlet pressure uniform, pressure dependent
profiles for radius and ulna (Figs. 4.23 and 4.24).
Using these velocity and pressure profiles as boundary conditions introduces the
direct and the reverse pressure waves. This approach may alleviate the difficulty of
including a downstream lumped hydrodynamic circuit to model the pressure reflec-
tions (Olufsen, 1999).

Structural analysis
The bones are a rigid, nondeformable structure therefore the pressure wave leads to struc-
tural changes in the vessel wall and the surrounding muscular tissue only, and these tissues
are assumed isotropic, almost incompressible. Their nonlinear deformations are modeled