Page 136 - Computational Statistics Handbook with MATLAB

Chapter 5: Exploratory Data Analysis 123

3

2

Sorted Y Values 1

0

−1

−2

−3
−3 −2 −1 0 1 2 3
Sample Quantiles − X
U
FI F IG URE G 5. RE 5. 8 8
F F II GU RE RE 5. 5. 8
GU
8
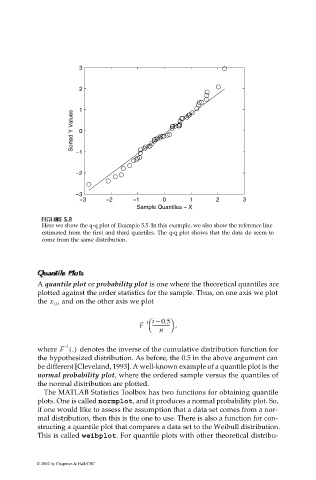
Here we show the q-q plot of Example 5.5. In this example, we also show the reference line
estimated from the first and third quartiles. The q-q plot shows that the data do seem to
come from the same distribution.

Qu
QuQu
annt
ilePlotPlot
ile
Qu aanntt tilePlotilePlots ss s
a
A quantile plot or probability plot is one where the theoretical quantiles are
plotted against the order statistics for the sample. Thus, on one axis we plot
the x i() and on the other axis we plot
–  0.5 
1 i –
F  ---------------  ,
n
where F () denotes the inverse of the cumulative distribution function for
1
–
.
the hypothesized distribution. As before, the 0.5 in the above argument can
be different [Cleveland, 1993]. A well-known example of a quantile plot is the
normal probability plot, where the ordered sample versus the quantiles of
the normal distribution are plotted.
The MATLAB Statistics Toolbox has two functions for obtaining quantile
plots. One is called normplot, and it produces a normal probability plot. So,
if one would like to assess the assumption that a data set comes from a nor-
mal distribution, then this is the one to use. There is also a function for con-
structing a quantile plot that compares a data set to the Weibull distribution.
This is called weibplot. For quantile plots with other theoretical distribu-

© 2002 by Chapman & Hall/CRC