Page 132 -

3.3 More neighborhood operators 111

(a) (b) (c)

(d) (e) (f)

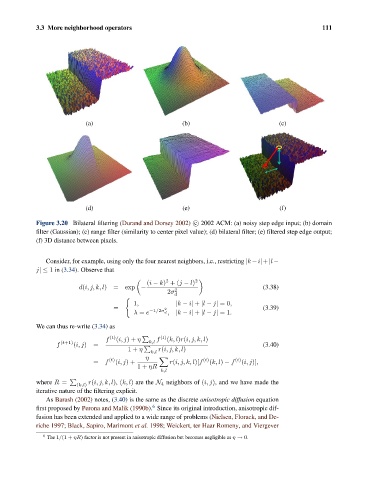
Figure 3.20 Bilateral filtering (Durand and Dorsey 2002) c 2002 ACM: (a) noisy step edge input; (b) domain
filter (Gaussian); (c) range filter (similarity to center pixel value); (d) bilateral filter; (e) filtered step edge output;
(f) 3D distance between pixels.

Consider, for example, using only the four nearest neighbors, i.e., restricting |k −i|+|l −
j|≤ 1 in (3.34). Observe that

2 2
(i − k) +(j − l)
d(i, j, k, l) = exp − 2 (3.38)
2σ
d

1, |k − i| + |l − j| =0,
= 2 (3.39)
λ = e −1/2σ d , |k − i| + |l − j| =1.
We can thus re-write (3.34)as
f (t) (i, j)+ η k,l f (t) (k, l)r(i, j, k, l)
f (t+1) (i, j)= (3.40)
1+ η r(i, j, k, l)
k,l
η (t) (t)
(t)
= f (i, j)+ r(i, j, k, l)[f (k, l) − f (i, j)],
1+ ηR
k,l
where R = r(i, j, k, l), (k, l) are the N 4 neighbors of (i, j), and we have made the
(k,l)
iterative nature of the filtering explicit.
As Barash (2002) notes, (3.40) is the same as the discrete anisotropic diffusion equation
6
first proposed by Perona and Malik (1990b). Since its original introduction, anisotropic dif-
fusion has been extended and applied to a wide range of problems (Nielsen, Florack, and De-
riche 1997; Black, Sapiro, Marimont et al. 1998; Weickert, ter Haar Romeny, and Viergever
6 The 1/(1 + ηR) factor is not present in anisotropic diffusion but becomes negligible as η → 0.