Page 310 - Design of Reinforced Masonry Structures

5.30 CHAPTER FIVE

3'' Calculate factored loads.
Load Combinations:
4#6
1. U = 1.4D = 1.4(10) = 140 kips
2. U = 1.2D + 1.6L = 1.2(100) + 1.6(175)
23.625'' #3@12 in. = 400 > 140 kips
P = 400 kips (governs)
u
fP = 400 kips
3'' n
3'' 3'' Check dimensions and h/t ratio for code compliance.
23.625''
Nominal column width = 24 in. > 8 in. OK
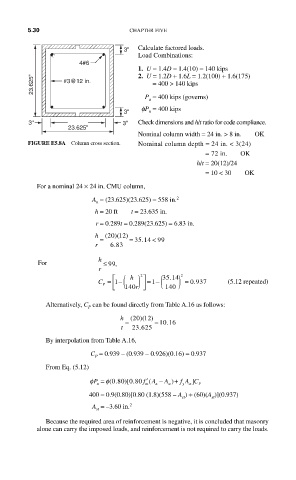
FIGURE E5.8A Column cross section. Nominal column depth = 24 in. < 3(24)
= 72 in. OK
h/t = 20(12)/24
= 10 < 30 OK

For a nominal 24 × 24 in. CMU column,
A = (23.625)(23.625) = 558 in. 2
n
h = 20 ft t = 23.635 in.
r = 0.289t = 0.289(23.625) = 6.83 in.
h (20 12
)( )
= = 35 .14 < 99
r . 683
h
For ≤ 99,
r
⎡ ( ) ⎥ ( ) 2
⎤
2
35 14
.
h
C = 1 − =− = 09 .337 (5.12 repeated)
1
⎢
P ⎣ 140 r ⎦ 140
Alternatively, C can be found directly from Table A.16 as follows:
P
12
h (20 )( )
= = 10 .16
t 23 .625
By interpolation from Table A.16,
C = 0.939 – (0.939 − 0.926)(0.16) = 0.937
P
From Eq. (5.12)
′
)
(
]
φP = φ(.080 )[.080 f A − A + f A C
st
y
P
st
n
m
n
400 = 0.9(0.80)[0.80 (1.8)(558 – A ) + (60)(A )](0.937)
st
st
A = –3.60 in. 2
st
Because the required area of reinforcement is negative, it is concluded that masonry
alone can carry the imposed loads, and reinforcement is not required to carry the loads.