Page 583 - Dynamics of Mechanical Systems

0593_C16_fm Page 564 Tuesday, May 7, 2002 7:06 AM

564 Dynamics of Mechanical Systems

and then from Eq. (16.13.1) we have:

x = r(θ sin ) θ and y = (1 ) θ (16.13.6)
−
r − cos
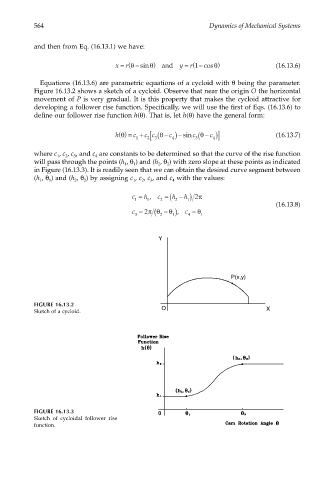
Equations (16.13.6) are parametric equations of a cycloid with θ being the parameter.
Figure 16.13.2 shows a sketch of a cycloid. Observe that near the origin O the horizontal
movement of P is very gradual. It is this property that makes the cycloid attractive for
developing a follower rise function. Specifically, we will use the first of Eqs. (16.13.6) to
define our follower rise function h(θ). That is, let h(θ) have the general form:

(
h θ () = c + c c θ − ) − sin c θ − )] (16.13.7)
c
c
1 2 ( [ 3 4 3 4
where c , c , c , and c are constants to be determined so that the curve of the rise function
2
3
4
1
will pass through the points (h , θ ) and (h , θ ) with zero slope at these points as indicated
1
1
2
2
in Figure (16.13.3). It is readily seen that we can obtain the desired curve segment between
(h , θ ) and (h , θ ) by assigning c , c , c , and c with the values:
2
4
1
2
2
3
1
1
c = h , c = ( h − ) 2π
h
1 1 2 2 1
(16.13.8)
c = 2πθ 2 ( − θ c = θ
3 1), 4 1
Y
P(x,y)
FIGURE 16.13.2 O
Sketch of a cycloid. X

FIGURE 16.13.3
Sketch of cycloidal follower rise
function.