Page 433 - Electrical Properties of Materials

Effect of negative material constants 415

0
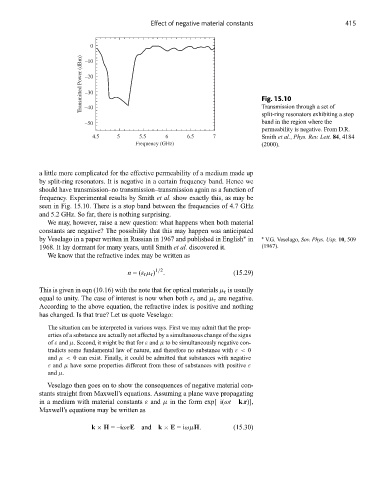
Transmitted Power (dBm) –20 Fig. 15.10
–10

–30

Transmission through a set of
–40
split-ring resonators exhibiting a stop
–50 band in the region where the
permeability is negative. From D.R.
4.5 5 5.5 6 6.5 7 Smith et al., Phys. Rev. Lett. 84, 4184
Frequency (GHz) (2000).

a little more complicated for the effective permeability of a medium made up
by split-ring resonators. It is negative in a certain frequency band. Hence we
should have transmission–no transmission–transmission again as a function of
frequency. Experimental results by Smith et al. show exactly this, as may be
seen in Fig. 15.10. There is a stop band between the frequencies of 4.7 GHz
and 5.2 GHz. So far, there is nothing surprising.
We may, however, raise a new question: what happens when both material
constants are negative? The possibility that this may happen was anticipated
by Veselago in a paper written in Russian in 1967 and published in English in ∗ V.G. Veselago, Sov. Phys. Usp. 10, 509
∗
1968. It lay dormant for many years, until Smith et al. discovered it. (1967).
We know that the refractive index may be written as

n =(ε r μ r ) 1/2 . (15.29)

This is given in eqn (10.16) with the note that for optical materials μ r is usually
equal to unity. The case of interest is now when both ε r and μ r are negative.
According to the above equation, the refractive index is positive and nothing
has changed. Is that true? Let us quote Veselago:
The situation can be interpreted in various ways. First we may admit that the prop-
erties of a substance are actually not affected by a simultaneous change of the signs
of ε and μ. Second, it might be that for ε and μ to be simultaneously negative con-
tradicts some fundamental law of nature, and therefore no substance with ε< 0
and μ< 0 can exist. Finally, it could be admitted that substances with negative
ε and μ have some properties different from those of substances with positive ε
and μ.
Veselago then goes on to show the consequences of negative material con-
stants straight from Maxwell’s equations. Assuming a plane wave propagating
in a medium with material constants ε and μ in the form exp[–i(ωt – k.r)],
Maxwell’s equations may be written as

k × H =–iωεE and k × E =iωμH. (15.30)