Page 435 - Electrical Properties of Materials

The ‘perfect’ lens 417

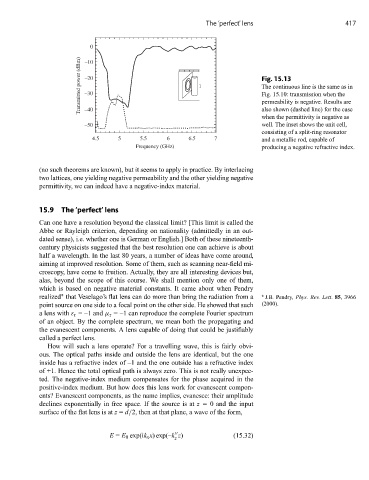
0
Transmitted power (dBm) –20 l Fig. 15.13
–10

The continuous line is the same as in
–30
Fig. 15.10: transmission when the
permeability is negative. Results are
also shown (dashed line) for the case
–40
when the permittivity is negative as
–50 well. The inset shows the unit cell,
consisting of a split-ring resonator
4.5 5 5.5 6 6.5 7 and a metallic rod, capable of
Frequency (GHz) producing a negative refractive index.

(no such theorems are known), but it seems to apply in practice. By interlacing
two lattices, one yielding negative permeability and the other yielding negative
permittivity, we can indeed have a negative-index material.

15.9 The ‘perfect’ lens
Can one have a resolution beyond the classical limit? [This limit is called the
Abbe or Rayleigh criterion, depending on nationality (admittedly in an out-
dated sense), i.e. whether one is German or English.] Both of these nineteenth-
century physicists suggested that the best resolution one can achieve is about
half a wavelength. In the last 80 years, a number of ideas have come around,
aiming at improved resolution. Some of them, such as scanning near-field mi-
croscopy, have come to fruition. Actually, they are all interesting devices but,
alas, beyond the scope of this course. We shall mention only one of them,
which is based on negative material constants. It came about when Pendry
∗
realized that Veselago’s flat lens can do more than bring the radiation from a ∗ J.B. Pendry, Phys.Rev.Lett. 85, 3966
point source on one side to a focal point on the other side. He showed that such (2000).
a lens with ε r = –1 and μ r = –1 can reproduce the complete Fourier spectrum
of an object. By the complete spectrum, we mean both the propagating and
the evanescent components. A lens capable of doing that could be justifiably
called a perfect lens.
How will such a lens operate? For a travelling wave, this is fairly obvi-
ous. The optical paths inside and outside the lens are identical, but the one
inside has a refractive index of –1 and the one outside has a refractive index
of +1. Hence the total optical path is always zero. This is not really unexpec-
ted. The negative-index medium compensates for the phase acquired in the
positive-index medium. But how does this lens work for evanescent compon-
ents? Evanescent components, as the name implies, evanesce: their amplitude
declines exponentially in free space. If the source is at z = 0 and the input
surface of the flat lens is at z = d/2, then at that plane, a wave of the form,

E = E 0 exp(ik x x)exp(–k z) (15.32)
z