Page 167 - Engineered Interfaces in Fiber Reinforced Composites

Chapter 4. Micromechanics ef stress transfer I49

end in a so-called ‘two-way debonding’ phenomenon. This phenomenon, peculiar to
the single fiber composite model as introduced in Section 4.3.1, has been studied
theoretically (Banbaji, 1988; Leung and Li, 1991, Hsueh, 1993; Hsueh and Becher,
1993) as well as experimentally for a relatively stiff fiber embedded in a soft matrix
(e.g. polyurethane matrix (Betz, 1982) and silicone resin (Gent and Liu, 1991)
reinforced with glass rods), which can satisfy the criterion given by Eq. (4.124).
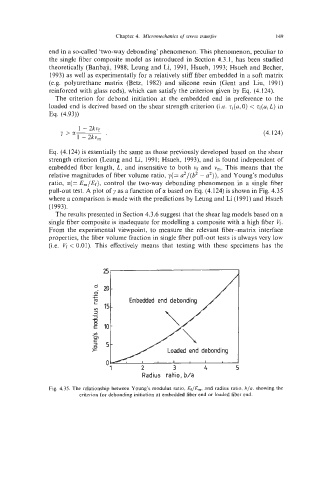
The criterion for debond initiation at the embedded end in preference to the
loaded end is derived based on the shear strength criterion (i.e. z,(u,O) < zi(a,L) in
Eq. (4.93))

1 - 2kvf
1
> ’ - 2kv, (4.124)
Eq. (4.124) is essentially the same as those previously developed based on the shear
strength criterion (Leung and Li, 1991; Hsueh, 1993), and is found independent of
embedded fiber length, L, and insensitive to both vf and v,. This means that the
relative magnitudes of fiber volume ratio, y(= a2/(b2 - a2)), and Young’s modulus
ratio, a(= E,/Ef), control the two-way debonding phenomenon in a single fiber
pull-out test. A plot of y as a function of a based on Eq. (4.124) is shown in Fig. 4.35
where a comparison is made with the predictions by Leung and Li (1991) and Hsueh
(1993).
The results presented in Section 4.3.6 suggest that the shear lag models based on a
single fiber composite is inadequate for modelling a composite with a high fiber 6.
From the experimental viewpoint, to measure the relevant fiber-matrix interface
properties, the fiber volume fraction in single fiber pull-out tests is always very low
(i.e. 6 < 0.01). This effectively means that testing with these specimens has the

2 3 4
Radius ratio, b/a

Fig. 4.35. The relationship between Young’s modulus ratio, Er/E,,,, and radius ratio, b/a, showing the
criterion for debonding initiation at embedded fiber end or loaded fiber end.