Page 128 - Fluid Mechanics and Thermodynamics of Turbomachinery

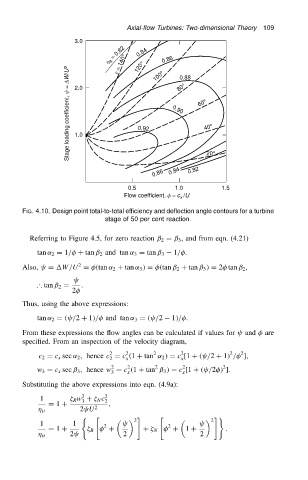
Axial-flow Turbines: Two-dimensional Theory 109
3.0
h tt = 0.82 120° 100° 0.86 0.88
0.84
e = 140°
Stage loading coefficient, y = DW/U 2 2.0 0.92 0.90 60° 40°

80°

1.0

0.86 0.84 0.82 20°

0.5 1.0 1.5
Flow coefficient, f = c /U
x
FIG. 4.10. Design point total-to-total efficiency and deflection angle contours for a turbine
stage of 50 per cent reaction.

Referring to Figure 4.5, for zero reaction ˇ 2 D ˇ 3 , and from eqn. (4.21)

1/ .
tan ˛ 2 D 1/ C tan ˇ 2 and tan ˛ 3 D tan ˇ 3
2
Also, D W/U D .tan ˛ 2 C tan ˛ 3 / D .tan ˇ 2 C tan ˇ 3 / D 2 tan ˇ 2 ,

∴ tan ˇ 2 D .
2

Thus, using the above expressions:
tan ˛ 2 D . /2 C 1// and tan ˛ 3 D . /2 1// .
From these expressions the flow angles can be calculated if values for and are
specified. From an inspection of the velocity diagram,
2
2
2
2
2
2
c 2 D c x sec ˛ 2 , hence c D c .1 C tan ˛ 2 / D c [1 C . /2 C 1/ / ],
2 x x
2
2
2
2
2
w 3 D c x sec ˇ 3 , hence w D c .1 C tan ˇ 3 / D c [1 C . /2 / ].
3 x x
Substituting the above expressions into eqn. (4.9a):
2
1 R w C N c 2 2
3
D 1 C 2 ,
tt 2 U
( " # " #)
2 2
1 1 2 2
D 1 C R C C N C 1 C .
tt 2 2 2