Page 308 - Fluid Mechanics and Thermodynamics of Turbomachinery

Hydraulic Turbines 289
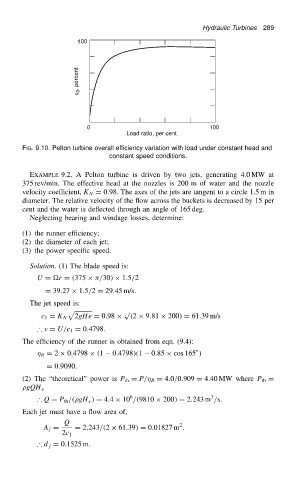
100

h 0 , percent

0 100
Load ratio, per cent

FIG. 9.10. Pelton turbine overall efficiency variation with load under constant head and
constant speed conditions.

EXAMPLE 9.2. A Pelton turbine is driven by two jets, generating 4.0 MW at
375 rev/min. The effective head at the nozzles is 200 m of water and the nozzle
velocity coefficient, K N D 0.98. The axes of the jets are tangent to a circle 1.5 m in
diameter. The relative velocity of the flow across the buckets is decreased by 15 per
cent and the water is deflected through an angle of 165 deg.
Neglecting bearing and windage losses, determine:
(1) the runner efficiency;
(2) the diameter of each jet;
(3) the power specific speed.

Solution. (1) The blade speed is:
U D r D .375 ð /30/ ð 1.5/2
D 39.27 ð 1.5/2 D 29.45 m/s.
The jet speed is:
p p
2gHe D 0.98 ð .2 ð 9.81 ð 200/ D 61.39 m/s
c 1 D K N
∴ D U/c 1 D 0.4798.
The efficiency of the runner is obtained from eqn. (9.4):
°
R D 2 ð 0.4798 ð .1 0.4798/.1 0.85 ð cos 165 /
D 0.9090.
(2) The “theoretical” power is P th D P/ R D 4.0/0.909 D 4.40 MW where P th D
gQH e
3
6
∴ Q D P th /. gH e / D 4.4 ð 10 /.9810 ð 200/ D 2.243 m /s.
Each jet must have a flow area of,
Q 2
A j D D 2.243/.2 ð 61.39/ D 0.01827 m .
2c 1
∴ d j D 0.1525 m.