Page 187 - Fundamentals of Communications Systems

Amplitude Modulation 6.9

w
1 2w
0.5
0.8
0.4
0.6 0.3
G xz (f) 0.4 G xc (f) 0.2

0.2 0.1

0 0
−0.2 −0.1
−3 −2 −1 0 1 2 3 −8 −6 −4 −2 0 2 4 6 8
Frequency, f, Hz Frequency, f, Hz
(a) Baseband spectrum (b) Bandpass spectrum
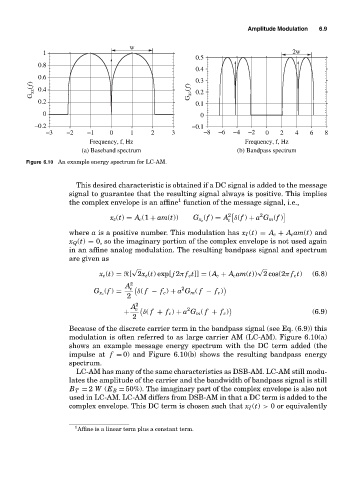
Figure 6.10 An example energy spectrum for LC-AM.

This desired characteristic is obtained if a DC signal is added to the message
signal to guarantee that the resulting signal always is positive. This implies
1
the complex envelope is an affine function of the message signal, i.e.,
2
2
x z (t) = A c (1 + am(t)) G x z (f ) = A δ(f ) + a G m (f )

c
where a is a positive number. This modulation has x I (t) = A c + A c am(t) and
x Q (t) = 0, so the imaginary portion of the complex envelope is not used again
in an affine analog modulation. The resulting bandpass signal and spectrum
are given as
√ √
x c (t) =
[ 2x z (t) exp[ j 2π f c t]] = (A c + A c am(t)) 2 cos(2π f c t) (6.8)
2
c
A 2
(f ) = δ( f − f c ) + a G m ( f − f c )
G x c
2
2
c 2
A
+ δ( f + f c ) + a G m ( f + f c ) (6.9)
2
Because of the discrete carrier term in the bandpass signal (see Eq. (6.9)) this
modulation is often referred to as large carrier AM (LC-AM). Figure 6.10(a)
shows an example message energy spectrum with the DC term added (the
impulse at f = 0) and Figure 6.10(b) shows the resulting bandpass energy
spectrum.
LC-AM has many of the same characteristics as DSB-AM. LC-AM still modu-
lates the amplitude of the carrier and the bandwidth of bandpass signal is still
B T = 2 W (E B = 50%). The imaginary part of the complex envelope is also not
used in LC-AM. LC-AM differs from DSB-AM in that a DC term is added to the
complex envelope. This DC term is chosen such that x I (t) > 0 or equivalently

1 Affine is a linear term plus a constant term.