Page 188 - Fundamentals of Communications Systems

6.10 Chapter Six

3
x (t) x z (t)
c
2
1

0

−1
−2

−3
0 5 10 15 20
Time
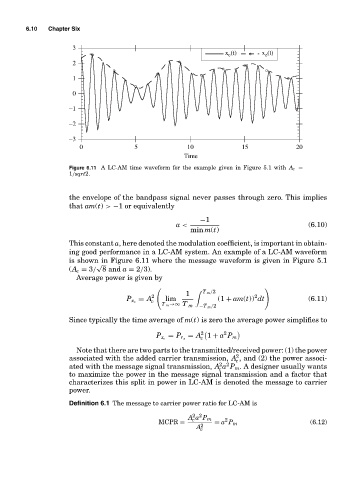
Figure 6.11 A LC-AM time waveform for the example given in Figure 5.1 with A c =
1/sqrt2.

the envelope of the bandpass signal never passes through zero. This implies
that am(t) > −1 or equivalently

−1
a < (6.10)
min m(t)
This constant a, here denoted the modulation coefficient, is important in obtain-
ing good performance in a LC-AM system. An example of a LC-AM waveform
is shown in Figure 6.11 where the message waveform is given in Figure 5.1
√
(A c = 3/ 8 and a = 2/3).
Average power is given by
# T m /2 $
1 2
2
= A lim (1 + am(t)) dt (6.11)
c
P x c
T m →∞ T m −T m /2
Since typically the time average of m(t) is zero the average power simplifies to
2 2
c
P x c = P r z = A 1 + a P m
Note that there are two parts to the transmitted/received power: (1) the power
2
associated with the added carrier transmission, A , and (2) the power associ-
c
2 2
ated with the message signal transmission, A a P m . A designer usually wants
c
to maximize the power in the message signal transmission and a factor that
characterizes this split in power in LC-AM is denoted the message to carrier
power.
Definition 6.1 The message to carrier power ratio for LC-AM is
2 2
A a P m 2
c
MCPR = = a P m (6.12)
A 2
c