Page 147 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

102 Fundamentals of Water Treatment Unit Processes: Physical, Chemical, and Biological

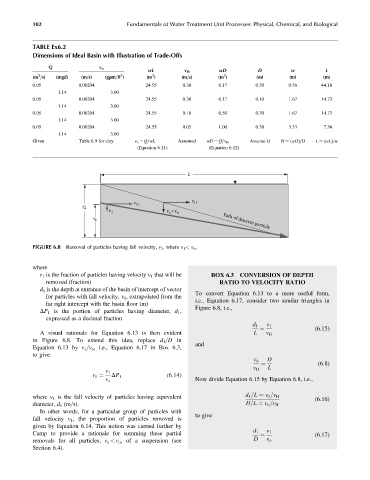
TABLE Ex6.2
Dimensions of Ideal Basin with Illustration of Trade-Offs
Q v o
wL v H wD D w L
2
3
2
2
(m =s) (mgd) (m=s) (gpm=ft ) (m ) (m=s) (m ) (m) (m) (m)
0.05 0.00204 24.55 0.30 0.17 0.30 0.56 44.18
1.14 3.00
0.05 0.00204 24.55 0.30 0.17 0.10 1.67 14.73
1.14 3.00
0.05 0.00204 24.55 0.10 0.50 0.30 1.67 14.73
1.14 3.00
0.05 0.00204 24.55 0.05 1.00 0.30 3.33 7.36
1.14 3.00
Given Table 6.9 for clay v o ¼ Q=wL Assumed wD ¼ Q=v H Assume D W ¼ (wD)=D L ¼ (wL)=w
(Equation 6.11) (Equation 6.12)

L

v H
v H
D
v 1 v =v o
s
d Path of discrete particle

FIGURE 6.8 Removal of particles having fall velocity, v 1 , where v 1 < v o .

where
r 1 is the fraction of particles having velocity v 1 that will be BOX 6.3 CONVERSION OF DEPTH
removed (fraction) RATIO TO VELOCITY RATIO
d 1 is the depth at entrance of the basin of intercept of vector
To convert Equation 6.13 to a more useful form,
for particles with fall velocity, v 1 , extrapolated from the
i.e., Equation 6.17, consider two similar triangles in
far right intercept with the basin floor (m)
Figure 6.8, i.e.,
DP 1 is the portion of particles having diameter, d 1 ,
expressed as a decimal fraction
d 1 v 1
(6:15)
¼
A visual rationale for Equation 6.13 is then evident L v H
in Figure 6.8. To extend this idea, replace d 1 =D in
and
Equation 6.13 by v 1 =v o , i.e., Equation 6.17 in Box 6.3,
to give
v o D
(6:8)
¼
v H L
v 1
DP 1 (6:14)
r 1 ¼
v o Now divide Equation 6.15 by Equation 6.8, i.e.,
where v 1 is the fall velocity of particles having equivalent d 1 =L ¼ v 1 =v H
(6:16)
diameter, d 1 (m=s). D=L ¼ v o =v H
In other words, for a particular group of particles with
to give
fall velocity v 1 , the proportion of particles removed is
given by Equation 6.14. This notion was carried further by
Camp to provide a rationale for summing these partial d 1 ¼ v 1 (6:17)
removals for all particles, v s < v o , of a suspension (see D v o
Section 6.4).