Page 446 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

Slow Sand Filtration 401

Slow sand has been termed, in fact, a ‘‘biological filter,’’ HLR (gpm/ft )
2
with the biofilm described as: ‘‘a teeming mass of micro- 0.01 0.1 1
organisms, bacteria, bacteriophages, predatory organisms 1.0
such as rotifers and protozoa, all feeding on the adsorbed 0.9
impurities and upon each other’’ (Huisman and Wood,
0.8
1974). Protozoa and Rotifera were found to be the dominant
interstitial microfauna removing bacteria within the sand bed 0.7
(Lloyd, 1973). Core sampling of the Hampton and Ashford 0.6 0.28 mm sand
Common filters in England showed aerobic bacteria,
flagellates, ciliates, rotifers, flatworms, gastrotrichs, nema- Removals (fraction) 0.5 0.78 mm sand
toda, annelida, and arthropoda (Duncan, 1988, p. 168). Bac- 0.4
9
10
terial densities were 10 –10 =mL sand; protozoans 0.3
(flagellates, ciliates [e.g., Vorticella], amoeba) numbered in
the thousands per mL. The Vorticella were considered the 0.2
most efficient ‘‘filter-feeders’’ of suspended particles. 0.1
The rate and extent of biofilm development increases Slow sand Rapid filtration
both with nutrient concentration and temperature (Bellamy 0.01 0.1 1 10
et al., 1985a,b; Barrett, 1989; Bryck et al., 1987a,b). Slow HLR (m/h)
sand filters located in a nutrient-limited situation may be
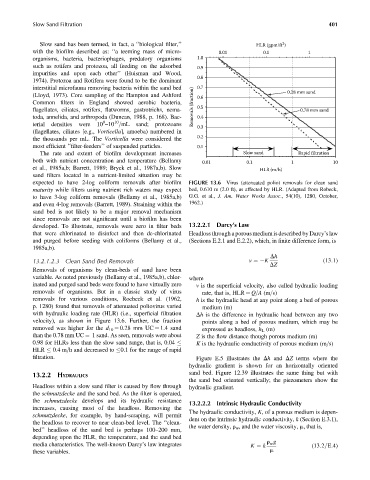
expected to have 2-log coliform removals after biofilm FIGURE 13.6 Virus (attenuated polio) removals for clean sand
maturity while filters using nutrient rich waters may expect bed, 0.610 m (2.0 ft), as affected by HLR. (Adapted from Robeck,
to have 3-log coliform removals (Bellamy et al., 1985a,b) G.G. et al., J. Am. Water Works Assoc., 54(10), 1280, October,
and even 4-log removals (Barrett, 1989). Straining within the 1962.)
sand bed is not likely to be a major removal mechanism
since removals are not significant until a biofilm has been
developed. To illustrate, removals were zero in filter beds 13.2.2.1 Darcy’s Law
that were chlorinated to disinfect and then de-chlorinated Headloss through a porous medium is described by Darcy’s law
and purged before seeding with coliforms (Bellamy et al., (Sections E.2.1 and E.2.2), which, in finite difference form, is
1985a,b).
Dh
13.2.1.2.3 Clean Sand Bed Removals v ¼ K (13:1)
DZ
Removals of organisms by clean-beds of sand have been
variable. As noted previously (Bellamy et al., 1985a,b), chlor- where
inated and purged sand beds were found to have virtually zero v is the superficial velocity, also called hydraulic loading
removals of organisms. But in a classic study of virus rate, that is, HLR ¼ Q=A (m=s)
removals for various conditions, Roebeck et al. (1962, h is the hydraulic head at any point along a bed of porous
p. 1280) found that removals of attenuated poliovirus varied medium (m)
with hydraulic loading rate (HLR) (i.e., superficial filtration Dh is the difference in hydraulic head between any two
velocity), as shown in Figure 13.6. Further, the fraction points along a bed of porous medium, which may be
removed was higher for the d 10 ¼ 0.28 mm UC ¼ 1.4 sand expressed as headloss, h L (m)
than the 0.78 mm UC ¼ 1 sand. As seen, removals were about Z is the flow distance though porous medium (m)
K is the hydraulic conductivity of porous medium (m=s)
0.98 for HLRs less than the slow sand range, that is, 0.04
HLR 0.4 m=h and decreased to 0.1 for the range of rapid
filtration. Figure E.5 illustrates the Dh and DZ terms where the
hydraulic gradient is shown for an horizontally oriented
sand bed. Figure 12.39 illustrates the same thing but with
13.2.2 HYDRAULICS
the sand bed oriented vertically; the piezometers show the
Headloss within a slow sand filter is caused by flow through hydraulic gradient.
the schmutzdecke and the sand bed. As the filter is operated,
the schmutzdecke develops and its hydraulic resistance
13.2.2.2 Intrinsic Hydraulic Conductivity
increases, causing most of the headloss. Removing the
The hydraulic conductivity, K, of a porous medium is depen-
schmutzdecke, for example, by hand-scraping, will permit
dent on the intrinsic hydraulic conductivity, k (Section E.3.1),
the headloss to recover to near clean-bed level. The ‘‘clean-
the water density, r w , and the water viscosity, m, that is,
bed’’ headloss of the sand bed is perhaps 100–200 mm,
depending upon the HLR, the temperature, and the sand bed
r g
media characteristics. The well-known Darcy’s law integrates K ¼ k w (13:2=E:4)
these variables. m