Page 95 - Geochemical Anomaly and Mineral Prospectivity Mapping in GIS

94 Chapter 4

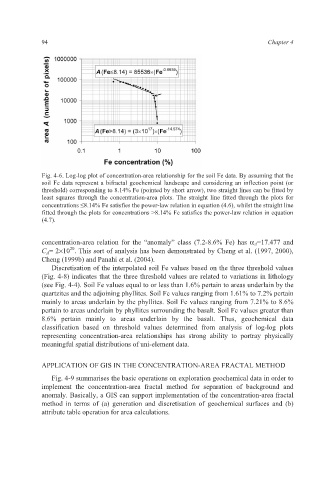
Fig. 4-6. Log-log plot of concentration-area relationship for the soil Fe data. By assuming that the
soil Fe data represent a bifractal geochemical landscape and considering an inflection point (or
threshold) corresponding to 8.14% Fe (pointed by short arrow), two straight lines can be fitted by
least squares through the concentration-area plots. The straight line fitted through the plots for
concentrations ≤8.14% Fe satisfies the power-law relation in equation (4.6), whilst the straight line
fitted through the plots for concentrations >8.14% Fe satisfies the power-law relation in equation
(4.7).

concentration-area relation for the “anomaly” class (7.2-8.6% Fe) has α A=17.477 and
20
C A= 2×10 . This sort of analysis has been demonstrated by Cheng et al. (1997, 2000),
Cheng (1999b) and Panahi et al. (2004).
Discretisation of the interpolated soil Fe values based on the three threshold values
(Fig. 4-8) indicates that the three threshold values are related to variations in lithology
(see Fig. 4-4). Soil Fe values equal to or less than 1.6% pertain to areas underlain by the
quartzites and the adjoining phyllites. Soil Fe values ranging from 1.61% to 7.2% pertain
mainly to areas underlain by the phyllites. Soil Fe values ranging from 7.21% to 8.6%
pertain to areas underlain by phyllites surrounding the basalt. Soil Fe values greater than
8.6% pertain mainly to areas underlain by the basalt. Thus, geochemical data
classification based on threshold values determined from analysis of log-log plots
representing concentration-area relationships has strong ability to portray physically
meaningful spatial distributions of uni-element data.

APPLICATION OF GIS IN THE CONCENTRATION-AREA FRACTAL METHOD
Fig. 4-9 summarises the basic operations on exploration geochemical data in order to
implement the concentration-area fractal method for separation of background and
anomaly. Basically, a GIS can support implementation of the concentration-area fractal
method in terms of (a) generation and discretisation of geochemical surfaces and (b)
attribute table operation for area calculations.