Page 143 - Innovations in Intelligent Machines

134 A. Pongpunwattana and R. Rysdyk
300
280
Expected value of loss function 240
260

220
200
180
160
140
120
100
0 20 40 60 80 100 120 140 160 180 200
Generation
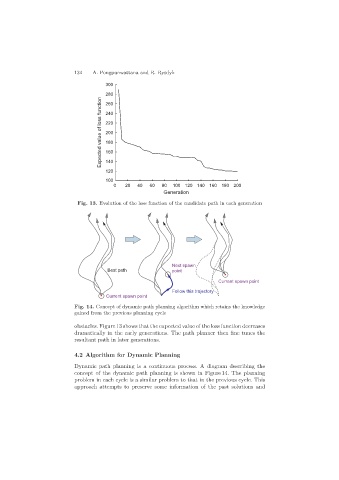
Fig. 13. Evolution of the loss function of the candidate path in each generation

Next spawn
Best path point
Current spawn point
Follow this trajectory
Current spawn point

Fig. 14. Concept of dynamic path planning algorithm which retains the knowledge
gained from the previous planning cycle

obstacles. Figure 13 shows that the expected value of the loss function decreases
dramatically in the early generations. The path planner then fine tunes the
resultant path in later generations.

4.2 Algorithm for Dynamic Planning

Dynamic path planning is a continuous process. A diagram describing the
concept of the dynamic path planning is shown in Figure 14. The planning
problem in each cycle is a similar problem to that in the previous cycle. This
approach attempts to preserve some information of the past solutions and