Page 131 - MATLAB an introduction with applications
P. 131
116 ——— MATLAB: An Introduction with Applications
semilogx(f,phase,‘Linewidth’,2);
%PHASE
title(‘\bfPlot of phase of current flow vs frequency’);
xlabel(‘\bfFrequency (Hz)’);
ylabel(‘\bfPhase (Deg)’);
grid on;
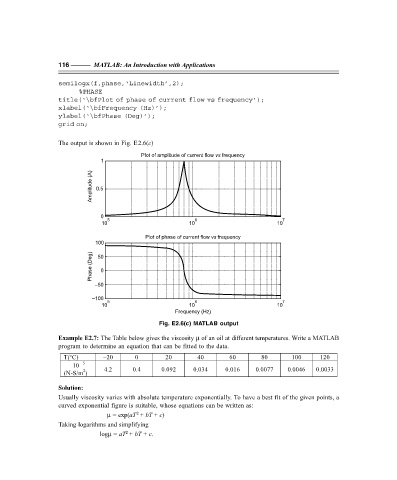
The output is shown in Fig. E2.6(c)
Plot of amplitude of current flow vs frequency
1
(A)
Amplitude 0.5
0
5 6 7
10 10 10
Plot of phase of current flow vs frequency
100
(Deg) 50
Phase 0
–50
–100
5 6 7
10 10 10
Frequency (Hz)
Fig. E2.6(c) MATLAB output
Example E2.7: The Table below gives the viscosity µ of an oil at different temperatures. Write a MATLAB
program to determine an equation that can be fitted to the data.
T(°C) –20 0 20 40 60 80 100 120
–5
10
2
(N-S/m ) 4.2 0.4 0.092 0.034 0.016 0.0077 0.0046 0.0033
Solution:
Usually viscosity varies with absolute temperature exponentially. To have a best fit of the given points, a
curved exponential figure is suitable, whose equations can be written as:
µ = exp(aT + bT + c)
2
Taking logarithms and simplifying
2
logµ = aT + bT + c.
F:\Final Book\Sanjay\IIIrd Printout\Dt. 10-03-09