Page 100 - MATLAB Recipes for Earth Sciences

5.3 Autospectral Analysis 93

Frequency Domain Time Domain
40
Main Lobe Rectangular
20 Side Lobes 1 Hanning
0 Rectangular
0.8
−20
Power (dB) −40 Amplitude 0.6 Bartlett
−60
−80 0.4
−100 Hanning
0.2
−120 Bartlett
−140 0
0 0.2 0.4 0.6 0.8 1.0 0 10 20 30 40 50 60
Frequency Time
a b
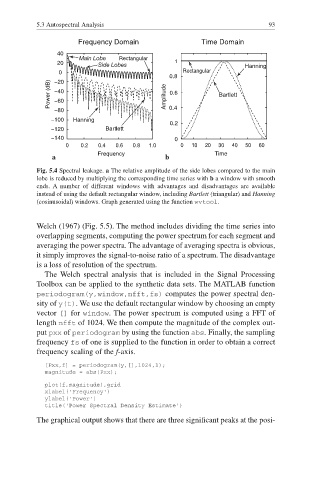
Fig. 5.4 Spectral leakage. a The relative amplitude of the side lobes compared to the main
lobe is reduced by multiplying the corresponding time series with b a window with smooth
ends. A number of different windows with advantages and disadvantages are available
instead of using the default rectangular window, including Bartlett (triangular) and Hanning
(cosinusoidal) windows. Graph generated using the function wvtool.

Welch (1967) (Fig. 5.5). The method includes dividing the time series into
overlapping segments, computing the power spectrum for each segment and
averaging the power spectra. The advantage of averaging spectra is obvious,
it simply improves the signal-to-noise ratio of a spectrum. The disadvantage
is a loss of resolution of the spectrum.
The Welch spectral analysis that is included in the Signal Processing
Toolbox can be applied to the synthetic data sets. The MATLAB function
periodogram(y,window,nfft,fs) computes the power spectral den-
sity of y(t). We use the default rectangular window by choosing an empty
vector [] for window. The power spectrum is computed using a FFT of
length nfft of 1024. We then compute the magnitude of the complex out-
put pxx of periodogram by using the function abs. Finally, the sampling
frequency fs of one is supplied to the function in order to obtain a correct
frequency scaling of the f-axis.

[Pxx,f] = periodogram(y,[],1024,1);
magnitude = abs(Pxx);
plot(f,magnitude),grid
xlabel('Frequency')
ylabel('Power')
title('Power Spectral Density Estimate')

The graphical output shows that there are three significant peaks at the posi-