Page 102 - MATLAB Recipes for Earth Sciences

5.3 Autospectral Analysis 95

plot(f,magnitude),grid
xlabel('Frequency')
ylabel('Power')
title('Power Spectral Density Estimate')

Let us increase the noise level. The gaussian noise has now a standard devia-
tion of five and zero mean.

randn('seed',0);
n = 5*randn(size(y));
yn = y + n;
[Pxx,f] = periodogram(yn,[],1024,1);
magnitude = abs(Pxx);
plot(f,magnitude), grid
xlabel('Frequency')
ylabel('Power')
title('Power Spectral Density Estimate')
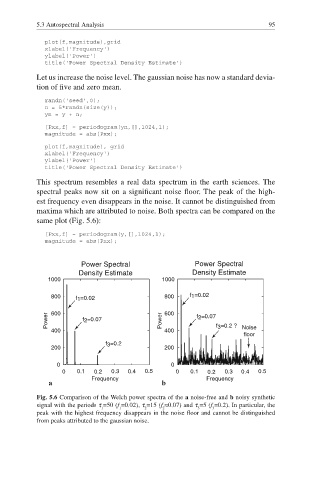
This spectrum resembles a real data spectrum in the earth sciences. The
spectral peaks now sit on a signifi cant noise floor. The peak of the high-

est frequency even disappears in the noise. It cannot be distinguished from
maxima which are attributed to noise. Both spectra can be compared on the
same plot (Fig. 5.6):
[Pxx,f] = periodogram(y,[],1024,1);
magnitude = abs(Pxx);

Power Spectral Power Spectral
Density Estimate Density Estimate
1000 1000

800 f 1 =0.02 800 f 1 =0.02

Power 600 f 2 =0.07 Power 600 f 2 =0.07

400 400 f 3 =0.2 ? Noise
floor
f 3 =0.2
200 200

0 0
0 0.1 0.2 0.3 0.4 0.5 0 0.1 0.2 0.3 0.4 0.5
Frequency Frequency
a b
Fig. 5.6 Comparison of the Welch power spectra of the a noise-free and b noisy synthetic
signal with the periods τ =50 (f =0.02), τ =15 (f §0.07) and τ =5 (f =0.2). In particular, the
1 1 2 2 3 3

peak with the highest frequency disappears in the noise floor and cannot be distinguished
from peaks attributed to the gaussian noise.