Page 169 - MODELING OF ASPHALT CONCRETE

Interr elationships among Asphalt Concr ete Stif fnesses 147

As concluded previously, the power-law series provides a globally smooth and
broadband representation of the LVE response data. Its main drawback is the associated
analytical difficulty when conducting mathematical operations. However, the latter fact
does not eliminate the importance of power-law series as an ideal candidate to
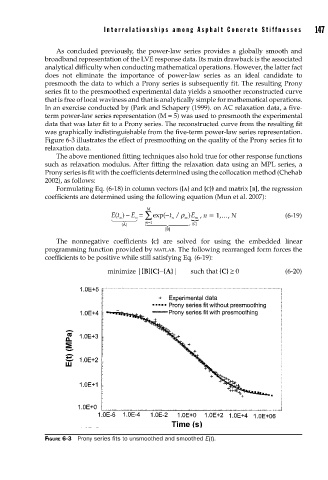
presmooth the data to which a Prony series is subsequently fit. The resulting Prony
series fit to the presmoothed experimental data yields a smoother reconstructed curve
that is free of local waviness and that is analytically simple for mathematical operations.
In an exercise conducted by (Park and Schapery (1999). on AC relaxation data, a five-
term power-law series representation (M = 5) was used to presmooth the experimental
data that was later fit to a Prony series. The reconstructed curve from the resulting fit
was graphically indistinguishable from the five-term power-law series representation.
Figure 6-3 illustrates the effect of presmoothing on the quality of the Prony series fit to
relaxation data.
The above mentioned fitting techniques also hold true for other response functions
such as relaxation modulus. After fitting the relaxation data using an MPL series, a
Prony series is fit with the coefficients determined using the collocation method (Chehab
2002), as follows:
Formulating Eq. (6-18) in column vectors ({A} and {C}) and matrix [B], the regression
coefficients are determined using the following equation (Mun et al. 2007):

∞ ∑
E
Et () − E = M exp(− t / ρ )E , n 1,…, N (6-19)
n m

m
n
m=1
{A} {C}
[B]
The nonnegative coefficients {C} are solved for using the embedded linear
programming function provided by MATLAB. The following rearranged form forces the
coefficients to be positive while still satisfying Eq. (6-19):
minimize |[B]{C}−{A}| such that {C} ≥ 0 (6-20)

FIGURE 6-3 Prony series fi ts to unsmoothed and smoothed E(t).