Page 170 - MODELING OF ASPHALT CONCRETE

148 Cha pte r S i x

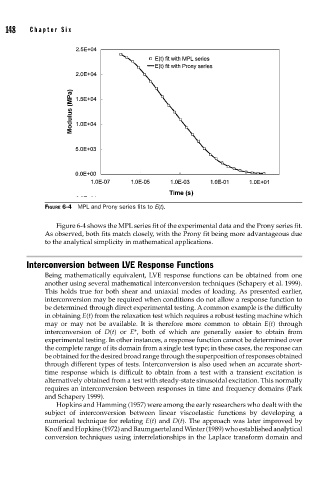
FIGURE 6-4 MPL and Prony series fi ts to E(t).

Figure 6-4 shows the MPL series fit of the experimental data and the Prony series fit.
As observed, both fits match closely, with the Prony fit being more advantageous due
to the analytical simplicity in mathematical applications.

Interconversion between LVE Response Functions
Being mathematically equivalent, LVE response functions can be obtained from one
another using several mathematical interconversion techniques (Schapery et al. 1999).
This holds true for both shear and uniaxial modes of loading. As presented earlier,
interconversion may be required when conditions do not allow a response function to
be determined through direct experimental testing. A common example is the difficulty
in obtaining E(t) from the relaxation test which requires a robust testing machine which
may or may not be available. It is therefore more common to obtain E(t) through
interconversion of D(t) or E*, both of which are generally easier to obtain from
experimental testing. In other instances, a response function cannot be determined over
the complete range of its domain from a single test type; in these cases, the response can
be obtained for the desired broad range through the superposition of responses obtained
through different types of tests. Interconversion is also used when an accurate short-
time response which is difficult to obtain from a test with a transient excitation is
alternatively obtained from a test with steady-state sinusoidal excitation. This normally
requires an interconversion between responses in time and frequency domains (Park
and Schapery 1999).
Hopkins and Hamming (1957) were among the early researchers who dealt with the
subject of interconversion between linear viscoelastic functions by developing a
numerical technique for relating E(t) and D(t). The approach was later improved by
Knoff and Hopkins (1972) and Baumgaertel and Winter (1989) who established analytical
conversion techniques using interrelationships in the Laplace transform domain and