Page 256 - Modern Control Systems

230 Chapter 3 State Variable Models

DESIGN PROBLEMS
CDP3.1 The traction drive uses the capstan drive system
- 5
f - r \ shown in Figure CDP2.1. Neglect the effect of the 0 K,
/ 1 1 ¾ motor inductance and determine a state variable
model for the system. The parameters are given in v = [-2 2]z.
Table CDP2.1. The friction of the slide is negligible.
DP3.1 A spring-mass-damper system, as shown in Figure
Determine the parameters a, b, and d to yield the re-
3.3, is used as a shock absorber for a large high-perfor-
quired diagonal matrix differential equation.
mance motorcycle. The original parameters selected
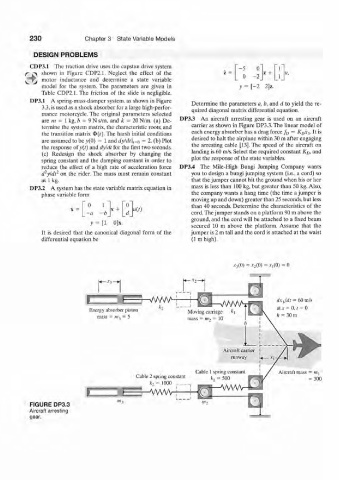
are m — 1 kg, b = 9 N s/m. and k = 20 N/m. (a) De- DP3.3 An aircraft arresting gear is used on an aircraft
termine the system matrix, the characteristic roots, and carrier as shown in Figure DP3.3. The linear model of
the transition matrix $(?)• The harsh initial conditions each energy absorber has a drag force f 0 = KQXT>. It is
are assumed to be v(0) = 1 and dy!dt\,=Q — 2. (b) Plot desired to halt the airplane within 30 m after engaging
the response oiy(t) and dyldt for the first two seconds. the arresting cable [13]. The speed of the aircraft on
(c) Redesign the shock absorber by changing the landing is 60 m/s. Select the required constant K D, and
spring constant and the damping constant in order to plot the response of the state variables.
reduce the effect of a high rate of acceleration force DP3.4 The Mile-High Bungi Jumping Company wants
2
d yldr on the rider. The mass must remain constant you to design a bungi jumping system (i.e., a cord) so
at'l kg. that the jumper cannot hit the ground when his or her
DP3.2 A system has the state variable matrix equation in mass is less than 100 kg, but greater than 50 kg. Also,
phase variable form the company wants a hang time (the time a jumper is
moving up and down) greater than 25 seconds, but less
0 1 than 40 seconds. Determine the characteristics of the
x + «(')
-a -b_ cord. The jumper stands on a platform 90 m above the
ground, and the cord will be attached to a fixed beam
v = [1 0]x.
secured 10 m above the platform. Assume that the
It is desired that the canonical diagonal form of the jumper is 2 m tall and the cord is attached at the waist
differential equation be (1 m high).

A',(0) = .r 2(0) = .v, (0) = 0
n r J:

V\AAAA dx\/dt = 60 m/s
L__j •Et; v W r
K a t - W
Energy absorber piston Moving carriage *i at x = 0, t = 0
mass = m, = 5 h = 30 m
mass = m-, = 10

Aircraft carrier
runway

Cable 1 spring constant
Cable 2 spring constant
h = 500
* 2 = 1000 AW
-vvwvj— S^
FIGURE DP3.3 « l 3
Aircraft arresting
gear.