Page 326 - Book Hosokawa Nanoparticle Technology Handbook

5.4 NANOPORE CHARACTERIZATION FUNDAMENTALS
the resultant distribution has bimodal or multimodal H1 H2
distribution.
5.4.3.4 Underestimation of pore size in
single-nanometer range
The spread of commercial nitrogen adsorption appa-
ratus has made PSD measurement quite easy. The
obtained PSDs, however, should not be blindly
accepted. The estimation of pore size based on the
Kelvin model as given by equations (5.4.3) and
(5.4.4) works well for pores larger than 10 nm. It has, H3 H4
however, been pointed out from late 1980s that the
model underestimates the so-called single-nanometer
range of pores [8, 9]. However, no method with sim-
plicity and convenience was available in even 1990s,
which forced people to use the Kelvin model though
knowing its inaccuracy.
A condensation model with simple concept and
easy calculation has recently been proposed [10, 11],
which is explained briefly in the following. The point
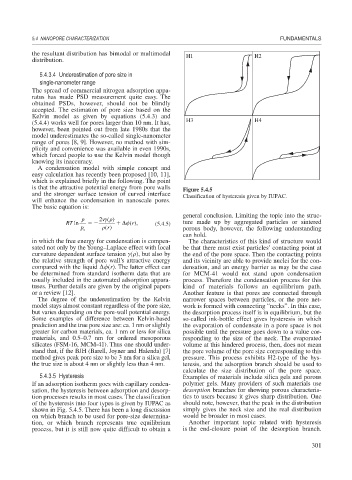
is that the attractive potential energy from pore walls Figure 5.4.5
and the stronger surface tension of curved interface Classification of hysteresis given by IUPAC.
will enhance the condensation in nanoscale pores.
The basic equation is:
general conclusion. Limiting the topic into the struc-
p 2 ()
RT ln r (), (5.4.5) ture made up by aggregated particles or sintered
p s r () porous body, however, the following understanding
can hold.
in which the free energy for condensation is compen- The characteristics of this kind of structure would
sated not only by the Young–Laplace effect with local be that there must exist particles’ contacting point at
curvature dependent surface tension ( ), but also by the end of the pore space. Then the contacting points
the relative strength of pore wall’s attractive energy and its vicinity are able to provide nuclei for the con-
compared with the liquid (r). The latter effect can densation, and an energy barrier as may be the case
be determined from standard isotherm data that are for MCM-41 would not stand upon condensation
usually included in the automated adsorption appara- process. Therefore the condensation process for this
tuses. Further details are given by the original papers kind of materials follows an equilibrium path.
or a review [12]. Another feature is that pores are connected through
The degree of the underestimation by the Kelvin narrower spaces between particles, or the pore net-
model stays almost constant regardless of the pore size, work is formed with connecting “necks”. In this case,
but varies depending on the pore-wall potential energy. the desorption process itself is in equilibrium, but the
Some examples of difference between Kelvin-based so-called ink-bottle effect gives hysteresis in which
prediction and the true pore size are: ca. 1 nm or slightly the evaporation of condensate in a pore space is not
greater for carbon materials, ca. 1 nm or less for silica possible until the pressure goes down to a value cor-
materials, and 0.5–0.7 nm for ordered mesoporous responding to the size of the neck. The evaporated
silicates (FSM-16, MCM-41). Thus one should under- volume at this hindered process, then, does not mean
stand that, if the BJH (Barell, Joyner and Halenda) [7] the pore volume of the pore size corresponding to this
method gives peak pore size to be 3 nm for a silica gel, pressure. This process exhibits H2-type of the hys-
the true size is about 4 nm or slightly less than 4 nm. teresis, and the adsorption branch should be used to
calculate the size distribution of the pore space.
5.4.3.5 Hysteresis Examples of materials include silica gels and porous
If an adsorption isotherm goes with capillary conden- polymer gels. Many providers of such materials use
sation, the hysteresis between adsorption and desorp- desorption branches for showing porous characteris-
tion processes results in most cases. The classification tics to users because it gives sharp distribution. One
of the hysteresis into four types is given by IUPAC as should note, however, that the peak in the distribution
shown in Fig. 5.4.5. There has been a long discussion simply gives the neck size and the real distribution
on which branch to be used for pore-size determina- would be broader in most cases.
tion, or which branch represents true equilibrium Another important topic related with hysteresis
process, but it is still now quite difficult to obtain a is the end-closure point of the desorption branch.

301