Page 94 - Book Hosokawa Nanoparticle Technology Handbook

FUNDAMENTALS CH. 2 STRUCTURAL CONTROL OF NANOPARTICLES

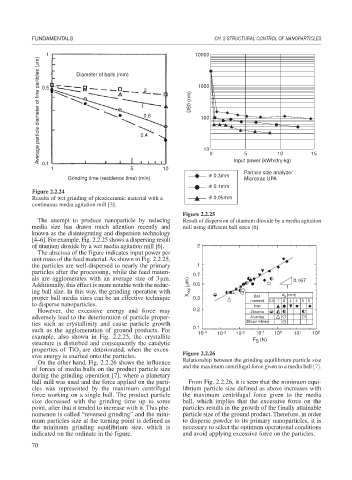
1 Diameter of balls (mm) 10000
Average particle diameter of fine particles ( m) 0.5 0.4 D50 (nm) 1000

2

1
0.6
100

5
10
0.1
1 5 10 10 0 Input power (kWh/dry . kg) 15
Particle size analyzer :
0.3mm
Grinding time (residence time) (min) Microtrac UPA
0.1mm
Figure 2.2.24
Results of wet grinding of piezoceramic material with a 0.05mm
continuous media agitation mill [3].
Figure 2.2.25
The attempt to produce nanoparticle by reducing Result of dispersion of titanium dioxide by a media agitation
media size has drawn much attention recently and mill using different ball sizes [6].
known as the disintegrating and dispersion technology
[4–6]. For example, Fig. 2.2.25 shows a dispersing result
of titanium dioxide by a wet media agitation mill [6]. 2
The abscissa of the figure indicates input power per
unit mass of the feed material. As shown in Fig. 2.2.25,
the particles are well-dispersed to nearly the primary 1
particles after the processing, while the feed materi-
als are agglomerates with an average size of 3 m. 0.167
Additionally, this effect is more notable with the reduc- X eql ( m) 0.7 1
0.5
ing ball size. In this way, the grinding operation with d [mm]
Ball
proper ball media sizes can be an effective technique 0.3 material 0.5 1 2 B 3 4 5 6
to disperse nanoparticles. Iron
However, the excessive energy and force may 0.2 Zirconia
adversely lead to the deterioration of particle proper- Alumina
ties such as crystallinity and cause particle growth 0.1 Silicon nitride
such as the agglomeration of ground products. For 10 -4 10 -3 10 -2 10 -1 10 0 10 1 10 2
example, also shown in Fig. 2.2.25, the crystallite F (N)
structure is disturbed and consequently the catalytic B
properties of TiO are deteriorated, when the exces-
2
sive energy is exerted onto the particles. Figure 2.2.26
On the other hand, Fig. 2.2.26 shows the influence Relationship between the grinding equilibrium particle size
of forces of media balls on the product particle size and the maximum centrifugal force given to a media ball [7].
during the grinding operation [7], where a planetary
ball mill was used and the force applied on the parti- From Fig. 2.2.26, it is seen that the minimum equi-
cles was represented by the maximum centrifugal librium particle size defined as above increases with
force working on a single ball. The product particle the maximum centrifugal force given to the media
size decreased with the grinding time up to some ball, which implies that the excessive force on the
point, after that it tended to increase with it. This phe- particles results in the growth of the finally attainable
nomenon is called “reversed grinding” and the mini- particle size of the ground product. Therefore, in order
mum particles size at the turning point is defined as to disperse powder to its primary nanoparticles, it is
the minimum grinding equilibrium size, which is necessary to select the optimum operational conditions
indicated on the ordinate in the figure. and avoid applying excessive force on the particles.
70