Page 139 - New Trends In Coal Conversion

102 New Trends in Coal Conversion

100 Hammer-milled:
Cumulative weight (wt%) 60 Roller-milled:
80
mean 360 µm
mean 900 µm
40
20
0
10 100 1,000 10,000
Particle size (µm)
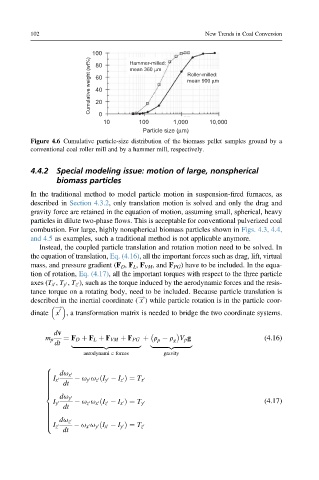
Figure 4.6 Cumulative particle-size distribution of the biomass pellet samples ground by a
conventional coal roller mill and by a hammer mill, respectively.

4.4.2 Special modeling issue: motion of large, nonspherical
biomass particles
In the traditional method to model particle motion in suspension-fired furnaces, as
described in Section 4.3.2, only translation motion is solved and only the drag and
gravity force are retained in the equation of motion, assuming small, spherical, heavy
particles in dilute two-phase flows. This is acceptable for conventional pulverized coal
combustion. For large, highly nonspherical biomass particles shown in Figs. 4.3, 4.4,
and 4.5 as examples, such a traditional method is not applicable anymore.
Instead, the coupled particle translation and rotation motion need to be solved. In
the equation of translation, Eq. (4.16), all the important forces such as drag, lift, virtual
mass, and pressure gradient (F D , F L , F VM , and F PG ) have to be included. In the equa-
tion of rotation, Eq. (4.17), all the important torques with respect to the three particle
axes (T x , T y , T z ), such as the torque induced by the aerodynamic forces and the resis-
0
0
0
tance torque on a rotating body, need to be included. Because particle translation is
!
described in the inertial coordinate ( x ) while particle rotation is in the particle coor-

!
0
dinate x , a transformation matrix is needed to bridge the two coordinate systems.

dv
m p ¼ F D þ F L þ F VM þ F PG þ r r V p g (4.16)
p
g
dt
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
aerodynami c forces gravity
8
> du x 0
>
> I x 0 u y u z ðI y I z Þ¼ T x 0
0
0
0
0
>
> dt
>
>
>
>
<
du y 0
I y 0 u z u x ðI z I x Þ¼ T y 0 (4.17)
0
0
0
0
> dt
>
>
>
>
>
> du z 0
>
>
: I z 0 u x u y ðI x I y Þ¼ T z 0
0
0
0
0
dt