Page 350 - Power Electronics Handbook

340 D.C. link frequency changers
1 .o I I I I I I 1 I I
-
0.9
0.8 -
c.
C -
g 0.7
a
0 . 0.6 -
v! -
4 0.5
U
p 0.4-
0
5 0.3-
U
0 -
6 0.2
-
0.1
Ib I I I I I I I
OO 20 30 40 50 60 70 80 90
Fundamental as % of d.c.
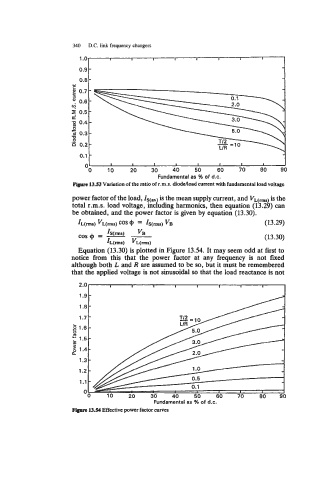
Ffye 13.53 Variation of the ratio of t.m.s. dioddoad current with fundamental load voltage
power factor of the load, is the mean supply current, and VL(-) is the
total r.m.s. load voltage, inciuding harmonics, then equation (13.29) can
be obtained, and the power factor is given by equation (13.30).
IL(rms) vL(rms) COS 4) = IS(rms) VB (13.29)
cos 4) = - - (13.30)
VB
IS(rms)
IL(rms) VL(rmS)
Equation (13.30) is plotted in Figure 13.54. It may seem odd at first to
notice from this that the power factor at any frequency is not fixed
although both L and R are assumed to be so, but it must be remembered
that the applied voltage is not sinusoidal so that the load reactance is not

2.0 I I I I I 8 I I
-
1.9
-
1.8
-
1.7'

Fundamental as 46 of d.c.
Figure 13.54 Effective power factor curves