Page 177 - Probability Demystified

166 CHAPTER 9 The Normal Distribution

SOLUTION:

Find the z value for 680:
value mean 680 500 180
z ¼ ¼ ¼ ¼ 1:8
standard deviation 100 100

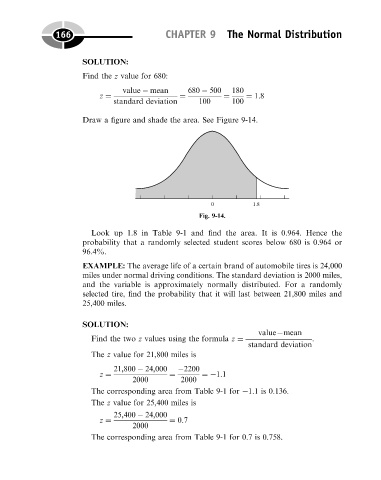
Draw a figure and shade the area. See Figure 9-14.

Fig. 9-14.

Look up 1.8 in Table 9-1 and find the area. It is 0.964. Hence the
probability that a randomly selected student scores below 680 is 0.964 or
96.4%.

EXAMPLE: The average life of a certain brand of automobile tires is 24,000
miles under normal driving conditions. The standard deviation is 2000 miles,
and the variable is approximately normally distributed. For a randomly
selected tire, find the probability that it will last between 21,800 miles and
25,400 miles.

SOLUTION:
value mean
Find the two z values using the formula z ¼ .
standard deviation
The z value for 21,800 miles is

21ó800 24ó000 2200
z ¼ ¼ ¼ 1:1
2000 2000
The corresponding area from Table 9-1 for 1.1 is 0.136.
The z value for 25,400 miles is
25ó400 24ó000
z ¼ ¼ 0:7
2000
The corresponding area from Table 9-1 for 0.7 is 0.758.