Page 249 - Rashid, Power Electronics Handbook
P. 249
238 J. Espinoza
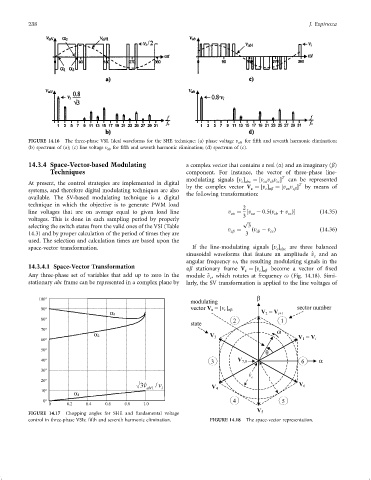
FIGURE 14.16 The three-phase VSI. Ideal waveforms for the SHE technique: (a) phase voltage v aN for ®fth and seventh harmonic elimination;
(b) spectrum of (a); (c) line voltage v ab for ®fth and seventh harmonic elimination; (d) spectrum of (c).
14.3.4 Space-Vector-based Modulating a complex vector that contains a real (a) and an imaginary (b)
Techniques component. For instance, the vector of three-phase line-
T
modulating signals v ¼v v v can be represented
c abc
ca cb cc
At present, the control strategies are implemented in digital T
by the complex vector V ¼v ¼v v by means of
systems, and therefore digital modulating techniques are also c c ab ca cb
the following transformation:
available. The SV-based modulating technique is a digital
technique in which the objective is to generate PWM load
2
line voltages that are on average equal to given load line v ¼ v ÿ 0:5ðv þ v Þ ð14:35Þ
ca
cc
cb
ca
voltages. This is done in each sampling period by properly 3 p
selecting the switch states from the valid ones of the VSI (Table 3
v cb ¼ ðv ÿ v Þ ð14:36Þ
cb
cc
14.3) and by proper calculation of the period of times they are 3
used. The selection and calculation times are based upon the
space-vector transformation. If the line-modulating signals v are three balanced
c abc
sinusoidal waveforms that feature an amplitude ^ v and an
c
angular frequency o, the resulting modulating signals in the
14.3.4.1 Space-Vector Transformation ab stationary frame V ¼v become a vector of ®xed
c c ab
Any three-phase set of variables that add up to zero in the module ^ v , which rotates at frequency o (Fig. 14.18). Simi-
c
stationary abc frame can be represented in a complex plane by larly, the SV transformation is applied to the line voltages of
v ˆ
c
v ˆ 3 aN1 v / i
FIGURE 14.17 Chopping angles for SHE and fundamental voltage
control in three-phase VSIs: ®fth and seventh harmonic elimination. FIGURE 14.18 The space-vector representation.