Page 90 - Renewable Energy Devices and System with Simulations in MATLAB and ANSYS

Three-Phase Photovoltaic Systems: Structures, Topologies, and Control 77

VCO
PD LF
V i V PD V LF ω΄ θ ΄ V΄
x k pd k vco + + 1/s cos
ω i

(a)
V ΄ αβ/dq
α
V α x LF VCO sin

V i – V q V ω + ω΄ θ ΄
QSG + + 1/s
V x ω i cos
β
V ΄
β

SOGI
V i – V e V α
+ k osg + – x 1/s
ω΄

x 1/s
V β
QSG

x –γ 1/s ++ ω i

FLL
(b)
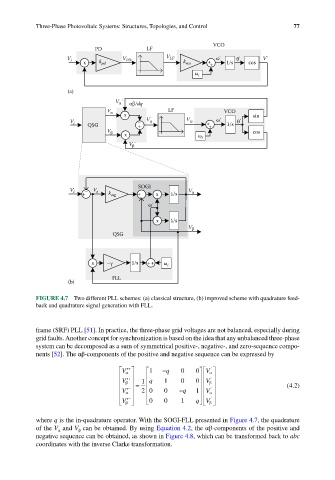
FIGURE 4.7 Two different PLL schemes: (a) classical structure, (b) improved scheme with quadrature feed-
back and quadrature signal generation with FLL.

frame (SRF) PLL [51]. In practice, the three-phase grid voltages are not balanced, especially during
grid faults. Another concept for synchronization is based on the idea that any unbalanced three-phase
system can be decomposed as a sum of symmetrical positive-, negative-, and zero-sequence compo-
nents [52]. The αβ-components of the positive and negative sequence can be expressed by
′  1 −q 0 ′ 
+
V α  0 V α
 +     ′ 
 ′ V β  = 1  q 1 0 0 V β  (4.2)
 
 ′  2 0 0 −q 1  ′ 
−
 V α −     V α ′ 
  
  ′ V β    0 0 1 q V β  
where q is the in-quadrature operator. With the SOGI-FLL presented in Figure 4.7, the quadrature
of the V and V can be obtained. By using Equation 4.2, the αβ-components of the positive and
β
α
negative sequence can be obtained, as shown in Figure 4.8, which can be transformed back to abc
coordinates with the inverse Clarke transformation.