Page 357 - Schaum's Outline of Theory and Problems of Advanced Calculus

348 FOURIER SERIES [CHAP. 13

f (x)
2

x
_ _
6 3 3 6
_
2
Fig. 13-8

From Fig. 13-9 below it is seen that the function is neither even nor odd.

f (x)
1

x
_ _ O
2p p p 2p 3p

Fig. 13-9

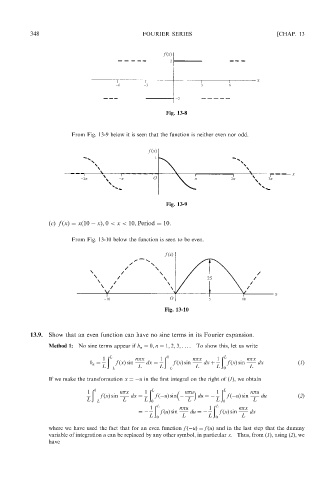
ðcÞ f ðxÞ¼ xð10 xÞ; 0 < x < 10; Period ¼ 10:

From Fig. 13-10 below the function is seen to be even.

f (x)

25

x
_ O
10 5 10
Fig. 13-10

13.9. Show that an even function can have no sine terms in its Fourier expansion.
Method 1: No sine terms appear if b n ¼ 0; n ¼ 1; 2; 3; .. . . Toshow this, let us write
1 ð L n x 1 ð 0 n x 1 ð L n x
f ðxÞ sin f ðxÞ sin f ðxÞ sin dx
b n ¼ dx ¼ dx þ ð1Þ
L L L L L L L 0 L
If we make the transformation x ¼ u in the first integral on the right of (1), we obtain

1 ð 0 n x 1 ð L n u 1 ð L n u
f ðxÞ sin dx ¼ f ð uÞ sin du ¼ f ð uÞ sin du ð2Þ
L L L L 0 L L 0 L
1 ð L n u 1 ð L n x
f ðuÞ sin f ðxÞ sin dx
¼ du ¼
L 0 L L 0 L
where we have used the fact that for an even function f ð uÞ¼ f ðuÞ and in the last step that the dummy
variable of integration u can be replaced by any other symbol, in particular x. Thus, from (1), using (2), we
have