Page 102 - Shigley's Mechanical Engineering Design

bud29281_ch03_071-146.qxd 11/30/2009 5:03 pm Page 77 pinnacle 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

Load and Stress Analysis 77
3–3 Singularity Functions

The four singularity functions defined in Table 3–1, using the angle brackets , consti-
tute a useful and easy means of integrating across discontinuities. By their use, general
expressions for shear force and bending moment in beams can be written when the beam
is loaded by concentrated moments or forces. As shown in the table, the concentrated
moment and force functions are zero for all values of x not equal to a. The functions are
undefined for values of x = a. Note that the unit step and ramp functions are zero only
for values of x that are less than a. The integration properties shown in the table con-
stitute a part of the mathematical definition too. The first two integrations of q(x) for
V(x) and M(x) do not require constants of integration provided all loads on the beam
are accounted for in q(x). The examples that follow show how these functions are used.

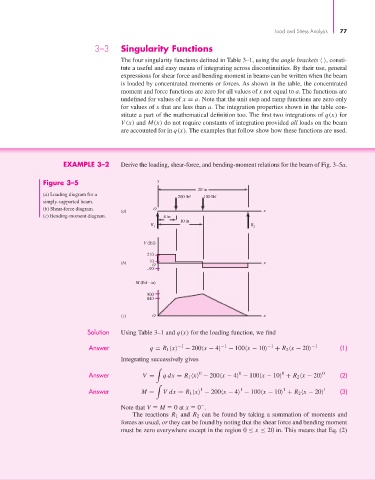
EXAMPLE 3–2 Derive the loading, shear-force, and bending-moment relations for the beam of Fig. 3–5a.

Figure 3–5 y
20 in
(a) Loading diagram for a
200 lbf 100 lbf
simply-supported beam.
(b) Shear-force diagram. O
(a) x
(c) Bending-moment diagram. 4 in
10 in
R R
1 2
V (lbf)
210
(b) 10 x
O
–90
M (lbf in)

900
840

(c) O x

Solution Using Table 3–1 and q(x) for the loading function, we find

Answer q = R 1 x −1 − 200 x − 4 −1 − 100 x − 10 −1 + R 2 x − 20 −1 (1)
Integrating successively gives

Answer V = qdx = R 1 x − 200 x − 4 − 100 x − 10 + R 2 x − 20 0 (2)
0
0
0

1
1
Answer M = Vdx = R 1 x − 200 x − 4 − 100 x − 10 + R 2 x − 20 1 (3)
1

Note that V M 0 at x 0 .
The reactions R 1 and R 2 can be found by taking a summation of moments and
forces as usual, or they can be found by noting that the shear force and bending moment
must be zero everywhere except in the region 0 ≤ x ≤ 20 in. This means that Eq. (2)