Page 474 - Shigley's Mechanical Engineering Design

bud29281_ch08_409-474.qxd 12/16/2009 7:11 pm Page 449 pinnacle 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

Screws, Fasteners, and the Design of Nonpermanent Joints 449
(b) Equation (8–30) gives the preload as

F i = 0.75F p = 0.75A t S p = 0.75(0.226)(85) = 14.4 kip
where from Table 8–9, S p = 85 kpsi for an SAE grade 5 cap screw. Using Eq. (8–28),
we obtain the load factor as the yielding factor of safety is

Answer n p = S p A t = 85(0.226) = 1.22
CP + F i 0.280(5) + 14.4
This is the traditional factor of safety, which compares the maximum bolt stress to the
proof strength.
Using Eq. (8–29),

85(0.226) − 14.4
S p A t − F i
Answer n L = = = 3.44
CP 0.280(5)
This factor is an indication of the overload on P that can be applied without exceeding
the proof strength.
Next, using Eq. (8–30), we have

14.4
F i
Answer n 0 = = = 4.00
P(1 − C) 5(1 − 0.280)
If the force P gets too large, the joint will separate and the bolt will take the entire
load. This factor guards against that event.
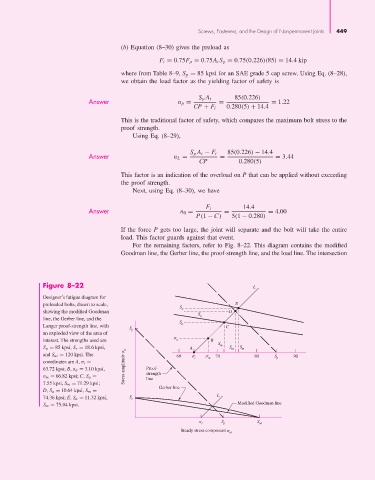
For the remaining factors, refer to Fig. 8–22. This diagram contains the modified
Goodman line, the Gerber line, the proof-strength line, and the load line. The intersection

Figure 8–22 L
Designer’s fatigue diagram for
preloaded bolts, drawn to scale, E
S a
showing the modified Goodman S D
line, the Gerber line, and the a
S
Langer proof-strength line, with a C
S
an exploded view of the area of p
interest. The strengths used are a B
S
S p = 85 kpsi, S e = 18.6 kpsi, A m S m S m
and S ut = 120 kpsi. The 60 i m 70 80 S p 90
coordinates are A, σ i =
63.72 kpsi; B, σ a = 3.10 kpsi, Stress amplitude a Proof-
σ m = 66.82 kpsi; C, S a = strength
line
7.55 kpsi, S m = 71.29 kpsi;
Gerber line
D, S a = 10.64 kpsi, S m =
74.36 kpsi; E, S a = 11.32 kpsi, S e L
S m = 75.04 kpsi. Modified Goodman line
S S
i p ut
Steady stress component
m