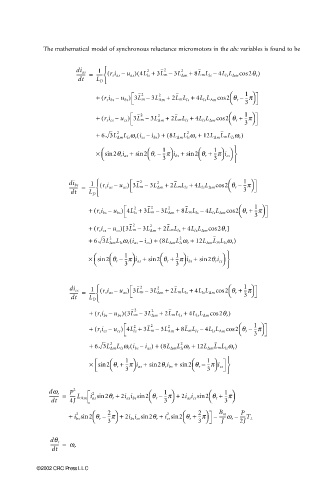Page 637 - The Mechatronics Handbook

0066_Frame_C20.fm Page 107 Wednesday, January 9, 2002 1:46 PM

The mathematical model of synchronous reluctance micromotors in the abc variables is found to be

1 
2
2
(
2
-------- = ------ ( r s i as – u as ) 4L ls + 3L m – 3L ∆m + 8L mL ls – 4L ls L ∆m cos 2q r )
di as

dt L D 

+ ( r s i bs – u bs ) 3L m – 3L ∆m + 2L mL ls + 4L ls L ∆m cos 2 q r – 1 --p 
2
2

3 

2
+ ( r s i cs – u cs ) 3L m – 3L ∆m + 2L mL ls + 4L ls L ∆m cos 2 q r + 1 
2
--p

3 
2
63L ∆m L ls w r i cs –(+ 2 i bs ) + ( 8L ∆m L ls w r + 12L ∆m L mL ls w r )



 
--p i bs +
×  sin 2q r i as + sin 2 q r – 1  sin 2 q r + 1 --p i cs 
  3   3   
1  2 2  1 
-------- = ------  ( r s i as – u as ) 3L m – 3L ∆m + 2L mL ls + 4L ls L ∆m cos 2 q r – --p
di bs

3 
dt L D 

2
+ ( r s i bs – u bs ) 4L ls + 3L m – 3L ∆m + 8L mL ls – 4L ls L ∆m cos 2 q r + 1 --p 
2
2
3 

2
+ ( r s i cs – u cs ) 3L m – 3L ∆m + 2L mL ls + 4L ls L ∆m cos 2q r ]
[
2
63L ∆m L ls w r i as –(+ 2 i cs ) + ( 8L ∆m L ls w r + 12L ∆m L mL ls w r )
2





×   sin 2 q r – 1 --p i as + sin 2 q r + 1  sin 2q r i cs 
--p i bs +

3 


3 

1  2 2  1 
-------- = ------  ( r s i as – u as ) 3L m – 3L ∆m + 2L mL ls + 4L ls L ∆m cos 2 q r + --p
di cs
3 

dt L D 
2
2
+ ( r s i bs – u bs ) 3L m – 3L ∆m + 2L mL ls + 4L ls L ∆m cos 2q r )
(

2
+ ( r s i cs – u cs ) 4L ls + 3L m – 3L ∆m + 8L mL ls – 4L ls L ∆m cos 2 q r – 1 
2
2
--p
 3 
2
63L ∆m L ls w r i bs –(+ 2 i as ) + ( 8L ∆m L ls w r + 12L ∆m L mL ls w r )


× sin 2 q r + 1  sin 2q r i bs + sin 2 q r – 1  
--p i as +
--p i cs 

3 

3 



--------- = P 2 2 2q r + 2i as i bs sin 2 q r – 1  2i as i cs sin 2 q r + 1 --p 
--p +
dw r
----- L ∆m i as sin
dt 4J  3   3 


P
--p +
2
+ i bs sin 2 q r – 2  2i bs i cs sin 2q r + i cs sin 2 q r + 2  – B m -----T L
2
--p
------w r –

3 
3 

2J
J
dq r
-------- =
dt w r
©2002 CRC Press LLC