Page 830 - The Mechatronics Handbook

066_Frame_C26 Page 15 Wednesday, January 9, 2002 1:59 PM

Accordingly, we want to make the ratio K c z c /p c as large as possible.
The characteristic equation is

(
(
2
2
(
c s() = ss + 3s + 3) sp c ) + K c s 3s + 3) sz c )
(
–
–
–
and it is desired to be in the form
(
c s() = ( s + 0.4) sr 3 ) sr 4 )
(
2
–
–
for some r 3,4 with Re(r 3,4 ) < 0, which implies that
d
c s() = 0, -----c s() = 0 (26.15)
s=−0.4 ds s=−0.4
Conditions (26.15) give two equations:
(
(
0.784 0.4 + p c ) 4.36K c 0.4 + ) = 0
–
z c
(
(
–
4.36K c – 0.784 1.08 0.4 + p c ) + 3.8K c 0.4 + ) = 0
z c
from which z c and p c can be solved in terms of K c . Then, by simple substitutions, the ratio to be maximized,
K c z c /p c , can be reduced to
3.4776K c – 0.784
--------- = ----------------------------------------------
K c z z
p c 24.2469K c – 3.4776
The maximizing value of K c is 0.1297; it leads to p c = −0.9508 and z c = −1.1637. For this controller, the
feedback system poles are

{ −1.64 + j0.37, 1.64 – j0.37, 0.40, 0.40 }
–
–
–
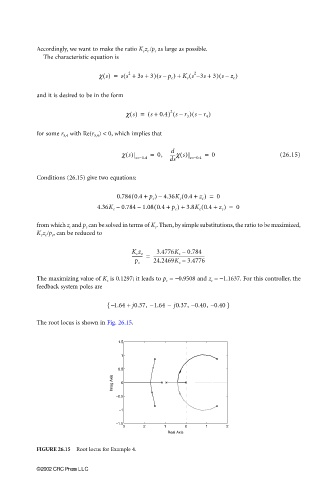
The root locus is shown in Fig. 26.15.

1.5

1
0.5
Imag Axis 0

−0.5

−1

−1.5
−3 −2 −1 0 1 2
Real Axis
FIGURE 26.15 Root locus for Example 4.

©2002 CRC Press LLC