Page 80 - Water Engineering Hydraulics, Distribution and Treatment

58
Chapter 3
Discharge
Time
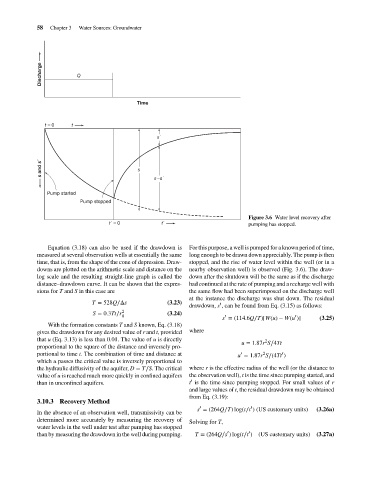
t = 0 t Q Water Sources: Groundwater
s´
s and s´ s

s–s´

Pump started
Pump stopped

Figure 3.6 Water level recovery after
t´ = 0 t´ pumping has stopped.

Equation (3.18) can also be used if the drawdown is For this purpose, a well is pumped for a known period of time,
measured at several observation wells at essentially the same long enough to be drawn down appreciably. The pump is then
time, that is, from the shape of the cone of depression. Draw- stopped, and the rise of water level within the well (or in a
downs are plotted on the arithmetic scale and distance on the nearby observation well) is observed (Fig. 3.6). The draw-
log scale and the resulting straight-line graph is called the down after the shutdown will be the same as if the discharge
distance–drawdown curve. It can be shown that the expres- had continued at the rate of pumping and a recharge well with
sions for T and S in this case are the same flow had been superimposed on the discharge well
at the instance the discharge was shut down. The residual
T = 528Q∕Δs (3.23) ′
drawdown, s , can be found from Eq. (3.15) as follows:
S = 0.3Tt∕r 2 (3.24)
0 ′ ′
s = (114.6Q∕T)[W(u) − W(u )] (3.25)
With the formation constants T and S known, Eq. (3.18)
gives the drawdown for any desired value of r and t, provided where
that u (Eq. 3.13) is less than 0.01. The value of u is directly 2
u = 1.87r S∕4Tt
proportional to the square of the distance and inversely pro-
portional to time t. The combination of time and distance at u = 1.87r S∕(4Tt )
′
2
′
which u passes the critical value is inversely proportional to
the hydraulic diffusivity of the aquifer, D = T∕S. The critical where r is the effective radius of the well (or the distance to
value of u is reached much more quickly in confined aquifers the observation well), t is the time since pumping started, and
′
than in unconfined aquifers. t is the time since pumping stopped. For small values of r
and large values of t, the residual drawdown may be obtained
from Eq. (3.19):
3.10.3 Recovery Method
′
′
s = (264Q∕T) log(t∕t ) (US customary units) (3.26a)
In the absence of an observation well, transmissivity can be
determined more accurately by measuring the recovery of Solving for T,
water levels in the well under test after pumping has stopped
′
′
than by measuring the drawdown in the well during pumping. T = (264Q∕s ) log(t∕t ) (US customary units) (3.27a)