Page 518 -

498 CHAPTER 12 SIMULATION

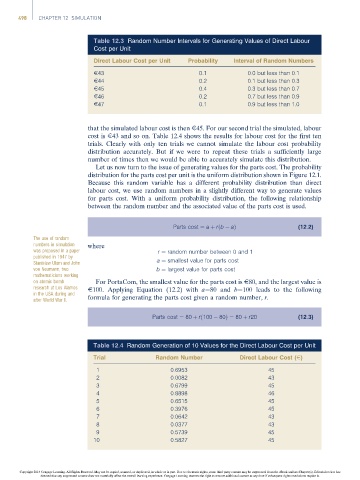
Table 12.3 Random Number Intervals for Generating Values of Direct Labour
Cost per Unit
Direct Labour Cost per Unit Probability Interval of Random Numbers

E43 0.1 0.0 but less than 0.1
E44 0.2 0.1 but less than 0.3
E45 0.4 0.3 but less than 0.7
E46 0.2 0.7 but less than 0.9
E47 0.1 0.9 but less than 1.0

that the simulated labour cost is then E45. For our second trial the simulated, labour
cost is E43 and so on. Table 12.4 shows the results for labour cost for the first ten
trials. Clearly with only ten trials we cannot simulate the labour cost probability
distribution accurately. But if we were to repeat these trials a sufficiently large
number of times then we would be able to accurately simulate this distribution.
Let us now turn to the issue of generating values for the parts cost. The probability
distribution for the parts cost per unit is the uniform distribution shown in Figure 12.1.
Because this random variable has a different probability distribution than direct
labour cost, we use random numbers in a slightly different way to generate values
for parts cost. With a uniform probability distribution, the following relationship
between the random number and the associated value of the parts cost is used.

Parts cost ¼ a þ rðb aÞ (12:2)

The use of random
numbers in simulation where
was proposed in a paper r ¼ random number between 0 and 1
published in 1947 by
Stanislaw Ulam and John a ¼ smallest value for parts cost
von Neumann, two b ¼ largest value for parts cost
mathematicians working
on atomic bomb For PortaCom, the smallest value for the parts cost is E80, and the largest value is
research at Los Alamos E100. Applying Equation (12.2) with a¼80 and b¼100 leads to the following
in the USA during and
after World War II. formula for generating the parts cost given a random number, r.

Parts cost ¼ 80 þ rð100 80Þ¼ 80 þ r20 (12:3)

Table 12.4 Random Generation of 10 Values for the Direct Labour Cost per Unit

Trial Random Number Direct Labour Cost (E)
1 0.6953 45
2 0.0082 43
3 0.6799 45
4 0.8898 46
5 0.6515 45
6 0.3976 45
7 0.0642 43
8 0.0377 43
9 0.5739 45
10 0.5827 45

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.