Page 48 - Biaxial Multiaxial Fatigue and Fracture

Evaluation of Fatigue of Fillet Welded Joints in Vehicle Components Under Multiaxial Service Loads 33

To determine the failure-critical element, damage calculations have been performed for
each element of the welding undercut. The critical element and corresponding fatigue lives
have been calculated applying three different multiaxial fatigue criteria. The first criterion -
maximum principal stress - is very suitable to limit the failure-critical region because of the
short computing time. Nevertheless, it is considered that life prediction should be based on a
critical plane criterion. In this investigation the same two critical plane criteria already used
for the hot spot stress approach - normal stress (mode I) and shear stress (mode II and III) -
are applied.
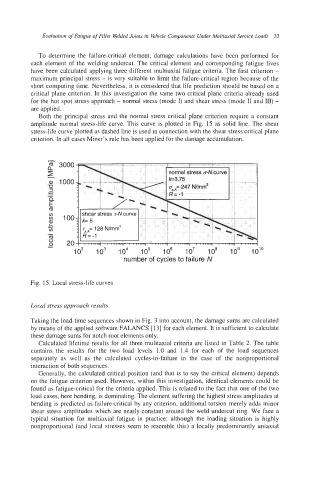
Both the principal stress and the normal stress critical plane criterion require a constant
amplitude normal stress-life curve. This curve is plotted in Fig. 15 as solid line. The shear
stress-life curve plotted as dashed line is used in connection with the shear stresscritical plane
criterion. In all cases Miner’s rule has been applied for the damage accumulation.

Fig. 15. Local stress-life curves

Local stress approach results
Taking the load-time sequences shown in Fig. 3 into account, the damage sums are calculated
by means of the applied software FALANCS [ 131 for each element. It is sufficient to calculate
these damage sums for notch root elements only.
Calculated lifetime results for all three mulitaxial criteria are listed in Table 2. The table
contains the results for the two load levels 1.0 and 1.4 for each of the load sequences
separately as well as the calculated cycles-to-failure in the case of the nonproportional
interaction of both sequences.
Generally, the calculated critical position (and that is to say the critical element) depends
on the fatigue criterion used. However, within this investigation, identical elements could be
found as fatigue-critical for the criteria applied. This is related to the fact that one of the two
load cases, here bending, is dominating. The element suffering the highest stress amplitudes at
bending is predicted as failure-critical by any criterion, additional torsion merely adds minor
shear stress amplitudes which are nearly constant around the weld undercut ring. We face a
typical situation for multiaxial fatigue in practice: although the loading situation is highly
nonproportional (and local stresses seem to resemble this) a locally predominantly uniaxial