Page 283 - Computational Statistics Handbook with MATLAB

272 Computational Statistics Handbook with MATLAB

axis([30 120 0 0.035])
xlabel('Waiting Time (minutes)')
ylabel('Probability Density Function')
title('Old Faithful-Waiting Times Between Eruptions')
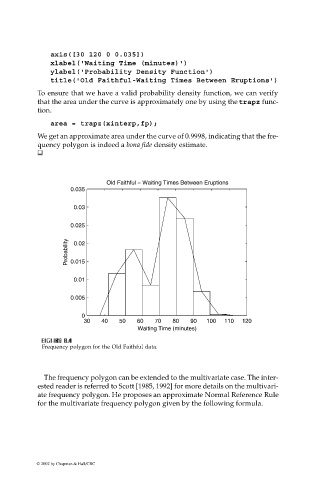
To ensure that we have a valid probability density function, we can verify
that the area under the curve is approximately one by using the trapz func-
tion.

area = trapz(xinterp,fp);
We get an approximate area under the curve of 0.9998, indicating that the fre-
quency polygon is indeed a bona fide density estimate.

Old Faithful − Waiting Times Between Eruptions
0.035

0.03

0.025
Probability 0.015
0.02

0.01

0.005

0
30 40 50 60 70 80 90 100 110 120
Waiting Time (minutes)

IG
F FI U URE G 8.4 RE 8.4
F F II GU RE RE 8.4
GU
8.4
Frequency polygon for the Old Faithful data.
The frequency polygon can be extended to the multivariate case. The inter-
ested reader is referred to Scott [1985, 1992] for more details on the multivari-
ate frequency polygon. He proposes an approximate Normal Reference Rule
for the multivariate frequency polygon given by the following formula.

© 2002 by Chapman & Hall/CRC