Page 570 - Dynamics of Mechanical Systems

0593_C16_fm Page 551 Tuesday, May 7, 2002 7:06 AM

Mechanical Components: Cams 551

Follower
Rise Dwell
h(t)
Dwell Dwell

0 Cam Rotation (Period T) T t
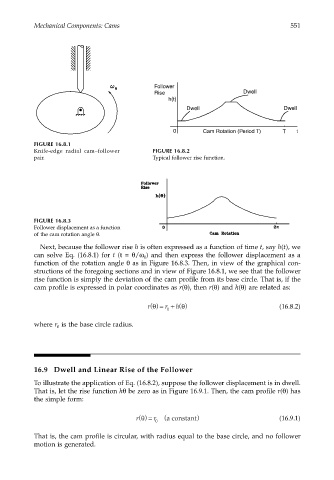
FIGURE 16.8.1
Knife-edge radial cam–follower FIGURE 16.8.2
pair. Typical follower rise function.

FIGURE 16.8.3
Follower displacement as a function
of the cam rotation angle θ.
Next, because the follower rise h is often expressed as a function of time t, say h(t), we
can solve Eq. (16.8.1) for t (t = θ/ω ) and then express the follower displacement as a
0
function of the rotation angle θ as in Figure 16.8.3. Then, in view of the graphical con-
structions of the foregoing sections and in view of Figure 16.8.1, we see that the follower
rise function is simply the deviation of the cam profile from its base circle. That is, if the
cam profile is expressed in polar coordinates as r(θ), then r(θ) and h(θ) are related as:

h θ
r θ () = r + () (16.8.2)
0
where r is the base circle radius.
0

16.9 Dwell and Linear Rise of the Follower
To illustrate the application of Eq. (16.8.2), suppose the follower displacement is in dwell.
That is, let the rise function hθ be zero as in Figure 16.9.1. Then, the cam profile r(θ) has
the simple form:

r θ () = r (a constant ) (16.9.1)
0
That is, the cam profile is circular, with radius equal to the base circle, and no follower
motion is generated.