Page 44 - Finite Element Modeling and Simulations with ANSYS Workbench

Bars and Trusses 29

y j x

Y u ′ i
i v i
u i

X

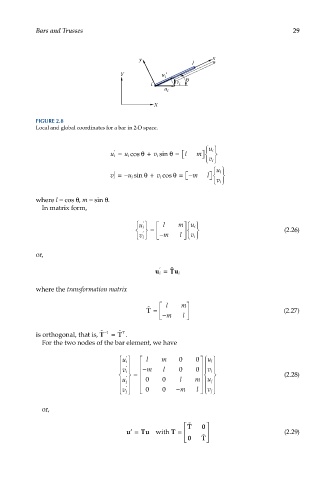
FIGURE 2.8
Local and global coordinates for a bar in 2-D space.

 u i 
′
u i = u i cos θ + v i sin θ =  l  m  

 v i 
 
u i

i
v i =− sin θ+ v i cos θ= −   m l  

u i
v i
 
where l = cos θ, m = sin θ.
In matrix form,
    l m 
′
u i 
u i
 ′  =  − m l    (2.26)
  v i     v i 
or,

′
u i = Tu i
where the transformation matrix

T =  l m   (2.27)

 −m l 
−1
T
is orthogonal, that is, T = T .
For the two nodes of the bar element, we have
′
   l m 0 0  u i 
i
u i
 ′    
i v
 v i   − m l 0 0  

 ′  =   (2.28)
 
 u j   0 0 l m u j


  0 0 − m l  
′
j v
v j
    
or,

T 0 
u ′ = Tu with T =   (2.29)

 0 T  