Page 108 - Instrumentation Reference Book 3E

Introduction 93

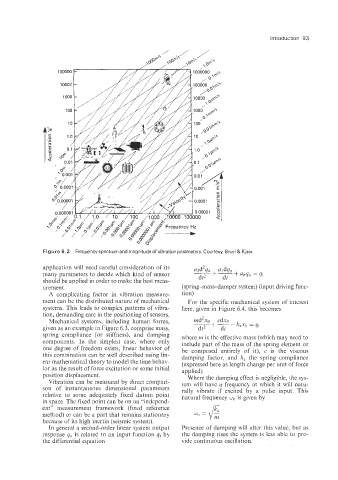
Figure 6.2 Frequency spectrum and magnitude of vibration parameters. Courtesy, Bruel & Kjaer.

application will need careful consideration of its
many parameters to decide which kind of sensor
should be applied in order to make the best meas-
urement. (spring-mass-damper system) (input driving func-
A complicating factor in vibration measure- tion)
ment can be the distributed nature of mechanical For the specific mechanical system of interest
systems. This leads to complex patterns of vibra- here, given in Figure 6.4, this becomes
tion, demanding care in the positioning of sensors.
Mechanical systems, including human forms, md2xo cdxo
given as an example in Figure 6.3, comprise mass, dt2 + dt - ksxo = 41
spring compliance (or stiffness), and damping where m is the effective mass (which may need to
components. In the simplest case, where only include part of the mass of the spring element or
one degree of freedom exists, linear behavior of
this combination can be well described using lin- be composed entirely of it), c is the vi ‘SCOUS
damping factor, and k, the spring compliance
ear mathematical theory to model the time behav- (expressed here as length change per unit of force
ior as the result of force excitation or some initial applied).
position displacement. Where the damping effect is negligible, the sys-
Vibration can be measured by direct compari- tem will have a frequency at which it will natu-
son of instantaneous dimensional parameters rally vibrate if excited by a pulse input. This
relative to some adequately fixed datum point natural frequency i~, is given by
in space. The fixed point can be on an “independ-
ent” measurement framework (fixed reference
method) or can be a part that remains stationary
because of its high inertia (seismic system).
In general a second-order linear system output Presence of damping will alter this value, but as
response qo is related to an input function qi by the damping rises the system is less able to pro-
the differential equation vide continuous oscillation.