Page 294 - Machine Learning for Subsurface Characterization

256 Machine learning for subsurface characterization

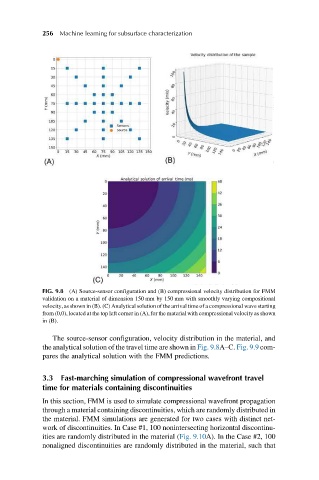
FIG. 9.8 (A) Source-sensor configuration and (B) compressional velocity distribution for FMM
validation on a material of dimension 150 mm by 150 mm with smoothly varying compositional
velocity, as shown in (B). (C) Analytical solution of the arrival time of a compressional wave starting
from (0,0), located at the top left corner in (A), for the material with compressional velocity as shown
in (B).

The source-sensor configuration, velocity distribution in the material, and
the analytical solution of the travel time are shown in Fig. 9.8A–C. Fig. 9.9 com-
pares the analytical solution with the FMM predictions.

3.3 Fast-marching simulation of compressional wavefront travel
time for materials containing discontinuities
In this section, FMM is used to simulate compressional wavefront propagation
through a material containing discontinuities, which are randomly distributed in
the material. FMM simulations are generated for two cases with distinct net-
work of discontinuities. In Case #1, 100 nonintersecting horizontal discontinu-
ities are randomly distributed in the material (Fig. 9.10A). In the Case #2, 100
nonaligned discontinuities are randomly distributed in the material, such that