Page 135 - MODELING OF ASPHALT CONCRETE

Complex Modulus Characterization of Asphalt Concr ete 113

The justification of using a sigmoidal function for fitting the compressive dynamic
modulus data is based on the physical observations of the mix behavior. The upper part
of the sigmoidal function approaches asymptotically to the maximum stiffness of the mix,
which is dependent on the limiting binder stiffness (glassy modulus) at cold temperatures.
At high temperatures, the compressive loading causes aggregate influence to be more
dominant than the viscous binder influence causing mix stiffness to approach a limiting
equilibrium value, which is dependent of the aggregate gradation. Thus, the sigmoidal
function captures the physical behavior of the asphalt mixtures observed in the mechanical
testing using compressive cyclic loading through the entire temperature range.
The advantage of using the sigmoidal fitting function is that a mastercurve can be
constructed using Excel spreadsheets and Solver Function. The Solver Function is a
tool for performing nonlinear least squares regression in the Excel spreadsheet.
However, it should be noted that if the dataset does not include modulus values for
full temperature range, caution should be used if the sigmoidal function is employed
in the mastercurve construction. One way is to confine the asymptotic high and low
modulus values to some assumed default values. Then, the asymptotic parameter
values d and d +a need to be constrained to proper modulus values to obtain adequate
mastercurve.
Witczak et al. (Fonseca and Witczak 1996; Andrei et al. 1999) introduced the
sigmoidal function to model the behavior of asphalt mixtures in conjunction with the
dynamic modulus predictive equation, which predicts mixture stiffness from volumetric
and raw material information.

Stress-Dependent Mastercurve for HMA
The stiffness of the hot mix asphalt (HMA) varies as a function of test temperature and
loading frequency as discussed above, however, the applied stress levels also affect the
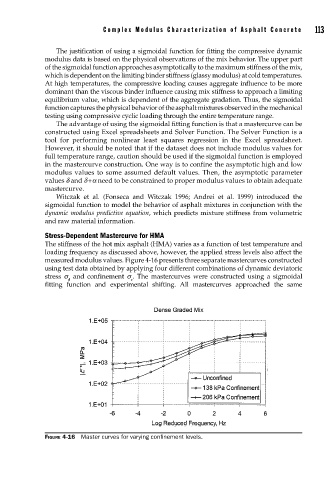
measured modulus values. Figure 4-16 presents three separate mastercurves constructed
using test data obtained by applying four different combinations of dynamic deviatoric
stress s and confinement s . The mastercurves were constructed using a sigmoidal
d c
fitting function and experimental shifting. All mastercurves approached the same

FIGURE 4-16 Master curves for varying confi nement levels.