Page 324 - Modern Control Systems

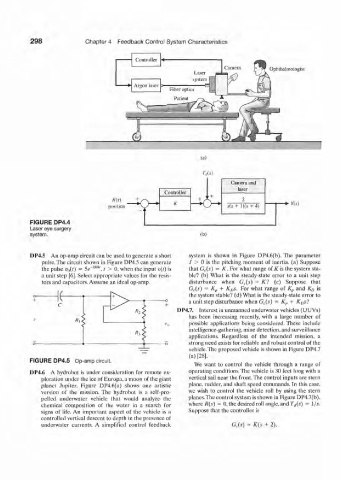
298 Chapter 4 Feedback Control System Characteristics

Controller
Camera Ophthalmologist
Laser
Argon laser Fiber optics t!

position -• Y(s)

FIGURE DP4.4
Laser eye surgery
system. (h)

DP4.5 An op-amp circuit can be used to generate a short system is shown in Figure DP4.6(b). The parameter
pulse. The circuit shown in Figure DP4.5 can generate ./ > 0 is the pitching moment of inertia, (a) Suppose
10
the pulse v n(t) = 5e~ '", r > 0, when the input v{i) is that GJs) = K, For what range of if is the system sta-
a unit step [6]. Select appropriate values for the resis- ble? (b) What is the steady-state error to a unit step
tors and capacitors. Assume an ideal op-amp. disturbance when G (.(s) = Kl (c) Suppose that
G t(s) = K p + Kj>s. For what range of K p and Ko is
K the system stable? (d) What is the steady-slate error to
a unit step disturbance when G c(s)
K 0s'l
+
=
K r
DP4.7. Interest in unmanned underwater vehicles (UUVs)
has been increasing recently, with a large number of
possible applications being considered. These include
intelligence-gathering, mine detection, and surveillance
applications. Regardless of the intended mission, a
strong need exists for reliable and robust control of the
vehicle. The proposed vehicle is shown in Figure DP4.7
(a) [28].
FIGURE DP4.5 Op-amp circuit.
We want to control the vehicle through a range of
DP4.6 A hydrobol is under consideration for remote ex- operating conditions. The vehicle is 30 feet long with a
ploration under the ice of Europa. a moon of the giant vertical sail near the front.The control inputs are stern
planet Jupiter. Figure DP4.6(a) shows one artistic plane, rudder, and shaft speed commands. In this case,
version of the mission. The hydrobot is a self-pro- we wish to control the vehicle roll by using the stern
pelled underwater vehicle that would analyze the planes. The control system is shown in Figure DP4.7(b),
chemical composition of the water in a search for where R(x) = 0, the desired roll angle, and T^s) = l/.v.
signs of life. An important aspect of the vehicle is a Suppose that the controller is
controlled vertical descent lo depth in the presence of
underwater currents. A simplified control feedback G,.(s) = K(s + 2).