Page 338 - Modern Control Systems

Chapter 5 The Performance of Feedback Control Systems

As nature would have it, these are contradictory requirements; thus, a compro-
mise must be obtained.To obtain an explicit relation for M pt and T p as a function of
£, one can differentiate Equation (5.9) and set it equal to zero. Alternatively, one
can utilize the differentiation property of the Laplace transform, which may be writ-
ten as

dy{t)
X \ w ^
-dTf = sY(s)

when the initial value of y(t) is zero. Therefore, we may acquire the derivative of y(t)
by multiplying Equation (5.8) by s and thus obtaining the right side of Equation
(5.10). Taking the inverse transform of the right side of Equation (5.10), we obtain
Equation (5.11), which is equal to zero when a) n(3t — ir. Thus, we find that the peak
time relationship for this second-order system is

T - " (5.14)
" "„Vi - C r

and the peak response is

• (5.15)
Therefore, the percent overshoot is
loot
is
P.O. = lOOe-W^. (5.16)

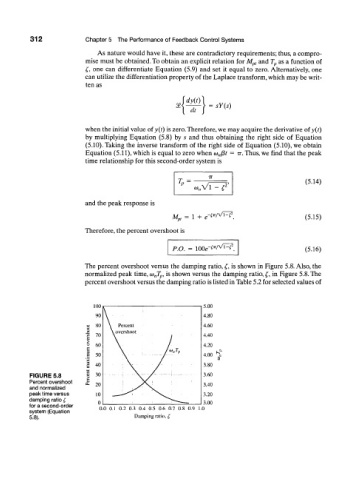
The percent overshoot versus the damping ratio, £, is shown in Figure 5.8. Also, the
normalized peak time, o) nT p, is shown versus the damping ratio, £, in Figure 5.8. The
percent overshoot versus the damping ratio is listed in Table 5.2 for selected values of

00 5.00
90 4.80
80 \ Percent 4.60
\ overshoot
70 4.40
60 4.20
50 l<»j v 4.00 K
3
40 3.80
FIGURE 5.8 30 ' 1— 3.60
Percent overshoot 20 y \ ' ! 3.40
and normalized
peak time versus 10 3.20
damping ratio £ 0 i
for a second-order 3.00
system (Equation 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Damping ratio, L,