Page 158 - Separation process principles 2

4.3 Azeotropic Systems 123

~f the pressures are sufficiently low that the equilibrium- 4.3 AZEOTROPIC SYSTEMS
vapor phase is ideal and the curve is convex, deviations from
Departures from Raoult's law frequently manifest them-
~aoult's law are positive, and species liquid-phase activity
selves in the formation of azeotropes, particularly for mix-
coefficients are greater than 1; if the curve is concave, devi-
tures of close-boiling species of different chemical types
ations are negative and activity coefficients are less than 1.
whose liquid solutions are nonideal. Azeotropes are formed
In either case, the total pressure is given by
by liquid mixtures exhibiting maximum- or minimum-
+
P = YAP~XA YBP~XB (4-7) boiling points. These represent, respectively, negative or pos-
itive deviations from Raoult's law. Vapor and liquid compo-
~f the vapor does not obey the ideal-gas law, (4-7) does not
sitions are identical at the azeotropic composition; thus, all
apply. In Figure 4.2~ system pressures are sufficiently high
K-values are 1 and no separation of species can take place.
that some deviation from the ideal-gas law occurs. However,
If only one liquid phase exists, the mixture forms a hom-
the convexity is due mainly to activity coefficients that are
ogeneous azeotrope; if more than one liquid phase is present,
greater than 1.
the azeotrope is heterogeneous. In accordance with the
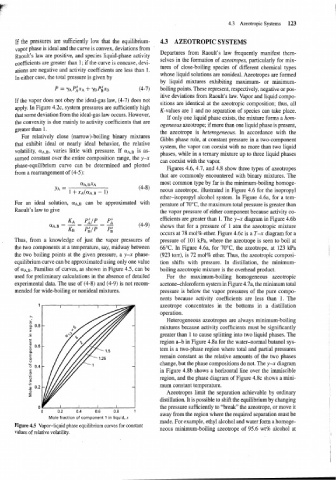
For relatively close (narrow)-boiling binary mixtures
Gibbs phase rule, at constant pressure in a two-component
that exhibit ideal or nearly ideal behavior, the relative
system, the vapor can coexist with no more than two liquid
volatility, CIA,B, varies little with pressure. If (YA,B is as-
phases, while in a ternary mixture up to three liquid phases
sumed constant over the entire composition range, the y-x
can coexist with the vapor.
phase-equilibrium curve can be determined and plotted
Figures 4.6, 4.7, and 4.8 show three types of azeotropes
from a rearrangement of (4-5):
that are commonly encountered with binary mixtures. The
most common type by far is the minimum-boiling homoge-
neous azeotrope, illustrated in Figure 4.6 for the isopropyl
ether-isopropyl alcohol system. In Figure 4.6a, for a tem-
For an ideal solution, aA,J can be approximated with perature of 70°C, the maximum total pressure is greater than
Raoult's law to give the vapor pressure of either component because activity co-
efficients are greater than 1. The y-x diagram in Figure 4.6b
shows that for a pressure of 1 atm the azeotropic mixture
occurs at 78 mol% ether. Figure 4.6~ is a T-x diagram for a
Thus, from a knowledge of just the vapor pressures of pressure of 101 kPa, where the azeotrope is seen to boil at
the two components at a temperature, say, midway between 66°C. In Figure 4.6a, for 70°C, the azeotrope, at 123 kPa I
the two boiling points at the given pressure, a y-x phase- (923 torr), is 72 mol% ether. Thus, the azeotropic composi- i
equilibrium curve can be approximated using only one value tion shifts with pressure. In distillation, the minimum-
of O~A,B. Families of curves, as shown in Figure 4.5, can be boiling azeotropic mixture is the overhead product.
used for preliminary calculations in the absence of detailed For the maximum-boiling homogeneous azeotropic
experimental data. The use of (4-8) and (4-9) is not recom- acetone-chloroform system in Figure 4.7a, the minimum total
mended for wide-boiling or nonideal mixtures. pressure is below the vapor pressures of the pure compo-
nents because activity coefficients are less than 1. The
azeotrope concentrates in the bottoms in a distillation
operation.
Heterogeneous azeotropes are always minimum-boiling
mixtures because activity coefficients must be significantly
greater than 1 to cause splitting into two liquid phases. The
region a-b in Figure 4.8a for the water-normal butanol sys-
tem is a two-phase region where total and partial pressures
remain constant as the relative amounts of the two phases
change, but the phase compositions do not. The y-x diagram
in Figure 4.8b shows a horizontal line over the immiscible
region, and the phase diagram of Figure 4.8~ shows a mini-
mum constant temperature.
Azeotropes limit the separation achievable by ordinary
distillation. It is possible to shift the equilibrium by changing
" the pressure sufficiently to "break" the azeotrope, or move it
0 0.2 0.4 0.6 0.8 1
away from the region where the required separation must be
Mole fraction of component 1 in liquid, x
made. For example, ethyl alcohol and water form a homoge-
Figure 4.5 Vapor-liquid phase equilibrium curves for constant neous minimum-boiling azeotrope of 95.6 wt% alcohol at
values of relative volatility.