Page 179 - Separation process principles 2

144 Chapter 4 Single Equilibrium Stages and Flash Calculations

SOLUTION condensed to a liquid. In this section, the physical equilib-
rium of gas-liquid mixtures is considered.
From the data given, c(~) 10 mrnolk, Q = 1 L, and S = 5 g.
=
Even though components of a gas mixture are at a tem-
(a) Graphical method. From (4-29), q; = - ($) CB + 10 (4) = perature above critical, they can dissolve in an appropriate
+
-0.2~~ 2
liquid solvent to an extent that depends on the temperature
This equation, with a slope of -0.2 and an intercept of 2, when and their partial pressure in the gas mixture. With good mix-
plotted on Figure 4.25, yields an intersection with the equilib-
ing, equilibrium between the two phases can be achieved in
rium curve at qi = 1.9 rnrnoYg and CB = 0.57 mmoMiter. a short time unless the liquid is very viscous.
Thus, the percent adsorption of phenol is
Unlike equilibrium vapor-liquid mixtures, where, as dis-
cussed in Chapter 2, a number of theoretical relationships
are in use for estimating K-values from molecular proper-
ties, no widely accepted theory exists for gas-liquid mix-
(b) Numerical algebraic method. Applying Eq. (1) from the prob- tures. Instead, experimental data, plots of experimental data,
lem statement and (4-31),
or empirical correlations are used.
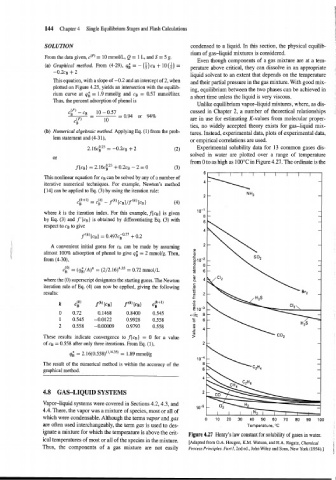
Experimental solubility data for 13 common gases dis-
solved in water are plotted over a range of temperature
from 0 to as high as 100°C in Figure 4.27. The ordinate is the

This nonlinear equation for c~ can be solved by any of a number of
iterative numerical techniques. For example, Newton's method
[14] can be applied to Eq. (3) by using the iteration rule:

where k is the iteration index. For this example, f{cB] is given
by Eq. (3) and ~'{cB] is obtained by differentiating Eq. (3) with
respect to CB to give

A convenient initial guess for CB can be made by assuming
almost 100% adsorption of phenol to give q;f = 2 mmol/g. Then,
from (4-30),

where the (0) superscript designates the starting guess. The Newton
iteration rule of Eq. (4) can now be applied, giving the following
results:

These results indicate convergence to flcB] = 0 for a value
of CB = 0.558 after only three iterations. From Eq. (I),

The result of the numerical method is within the accuracy of the
graphical method.

4.8 GAS-LIQUID SYSTEMS
Vapor-liquid systems were covered in Sections 4.2,4.3, and
4.4. There, the vapor was a mixture of species, most or all of
which were condensable. Although the terms vapor and gas 0 10 20 30 40 50 60 70 80 90 100
are often used interchangeably, the term gas is used to des- Temperature, "C
ignate a mixture for which the temperature is above the crit-
Figure 4.27 Henry's law constant for solubility of gases in water.
ical temperatures of most or all of the species in the mixture.
[Adapted from O.A. Hougen, K.M. Watson, and R.A. Ragatz, Chemical i
Thus, the components of a gas mixture are not easily Process Principles. Parrl, 2nd ed., John Wiley and Sons, New York (1954).] '
I