Page 175 - Separation process principles 2

140 Chapter 4 Single Equilibrium Stages and Flash Calc~~lations

before leaching, the soybeans are flaked to reduce the time required 5.0 I I I I
for mass transfer of the oil out of the bean and into hexane. Fol- 4.5 - -
lowing leaching, the hexane in the overflow is separated from the 1 F
'0
soy oil and recovered for recycle by evaporation, while the under- '5 4.0 -
u
flow is treated to remove residual hexane and toasted with '-
3.5 -
high-temperature air to produce defatted meal. Modem soybean-
extraction plants crush up to 3,000 tons of soybeans per day. This ! 3.0 -
E
example is concerned with just the leaching step. \ -
2 2.5 -
Oil is to be leached from 100,000 kgh of soybean flakes, con- g
taining 19% by weight oil, in a single stage by 100,000 kgh of a ; -
2.0
hexane solvent. Experimental data indicate that the oil content of
the flakes will be reduced to 0.5 wt%. For the type of equipment to 2
be used, the expected contents of the underflows is as follows:
-
p, Mass fraction of 0.68 0.67 0.65 0.62 0.58 0.53
solids in underflow I Overflow I
0 0.2 0.4 0.6 0.8 1
Mass ratio of 0.0 0.2 0.4 0.6 0.8 1.0
X,, Mass solute/mass of liquid
solute in underflow
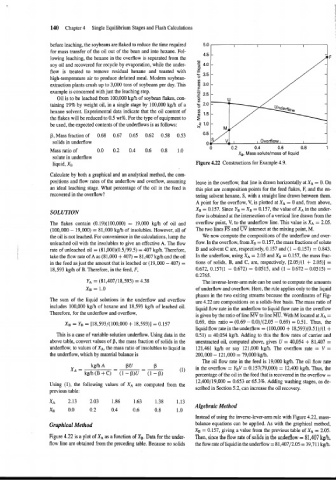
liquid, XB Figure 4.22 Constructions for Example 4.9.
Calculate by both a graphical and an analytical method, the com-
positions and flow rates of the underflow and overflow, assuming leave in the overflow, that line is drawn horizontally at XA = 0. On
an ideal leaching stage. What percentage of the oil in the feed is this plot are composition points for the feed flakes, F, and the en-
recovered in the overflow? tering solvent hexane, S, with a straight line drawn between them.
A point for the overflow, V, is plotted at XA = 0 and, from above,
XB = 0.157. Since YB = XB = 0.157, the value of XA in the under-
SOLUTION
flow is obtained at the intersection of a vertical line drawn from the
The flakes contain (0.19)(100,000) = 19,000 kgh of oil and overflow point, V, to the underflow line. This value is XA = 2.05.
(100,000 - 19,000) = 81,000 kgh of insolubles. However, all of The two lines % and intersect at the mixing point, M.
the oil is not leached. For convenience in the calculations, lump the We now compute the compositions of the underflow and over-
unleached oil with the insolubles to give an effective A. The flow flow. In the overflow, from XB = 0.157, the mass fractions of solute
I rate of unleached oil = (81,000)(0.5/99.5) = 407 kgh. Therefore, B and solvent C are, respectively, 0.157 and (1 - 0.157) = 0.843.
take the flow rate of A as (8 1,000 + 407) = 8 1,407 kgh and the oil In the underflow, using XA = 2.05 and XB = 0.157, the mass frac-
in the feed as just the amount that is leached or (19,000 - 407) = tions of solids, B, and C, are, respectively, [2.05/(1 + 2.05)] =
18,593 kgh of B. Therefore, in the feed, F, 0.672, 0.157(1 - 0.672) = 0.0515, and (1 - 0.672 - 0.0515) =
0.2765.
The inverse-lever-arm rule can be used to compute the amounts
of underflow and overflow. Here, the rule applies only to the liquid
phases in the two exiting streams because the coordinates of Fig-
The sum of the liquid solutions in the underflow and overflow
ure 4.22 are compositions on a solids-free basis. The mass ratio of
includes 100,000 kgh of hexane and 18,593 kgh of leached oil.
liquid flow rate in the underflow to liquid flow rate in the overflow
Therefore, for the underflow and overflow,
is given by the ratio of line to line MU. With M located at XA =
0.69, this ratio = (0.69 - 0.0)/(2.05 - 0.69) = 0.5 1. Thus, the
liquid flow rate in the underflow = (100,000 + 18,593)(0.5 1)/(1 +
This is a case of variable-solution underflow. Using data in the 0.51) = 40,054 kgh. Adding to this the flow rates of carrier and
above table, convert values of P, the mass fraction of solids in the unextracted oil, computed above, gives U = 40,054 + 81,407 =
underflow, to values of XA, the mass ratio of insolubles to liquid in 121,461 kgh or say 121,000 kgh. The overflow rate = V =
the underflow, which by material balance is 200,000 - 121,000 = 79,000 kgh.
The oil flow rate in the feed is 19,000 kgh. The oil flow rate
kgh A PU P
XA = in the overflow = YBV = 0.157(79,000) = 12,400 kgh. Thus, the
kgh (B +C) (1 - P)U (L-P) (1) percentage of the oil in the feed that is recovered in the overflow =
12,400/19,000 = 0.653 or 65.3%. Adding washing stages, as de-
Using (I), the following values of XA are computed from the
scribed in Section 5.2, can increase the oil recovery.
previous table:
XA 2.13 2.03 1.86 1.63 1.38 1.13
Algebraic Method
XB 0.0 0.2 0.4 0.6 0.8 1 .O
Instead of using the inverse-lever-arm rule with Figure 4.22, mass-
Graphical Method balance equations can be applied. As with the graphical method,
XB = 0.157, giving a value from the previous table of XA = 2.05.
Figure 4.22 is a plot of XA as a function of XB. Data for the under- Then, since the flow rate of solids in the underflow = 81,407 kglh,
flow line are obtained from the preceding table. Because no solids the flow rate of liquid in the underflow = 8 1,40712.05 = 39,7 11 kglh.